In this page we present some basic information about neutrinos. This is designed for anyone with a general interest in particle physics – we hope it will be useful to anyone who’s interested enough to be reading these pages, regardless of whether or not you studied physics at high school!
For information on particle physics and the Standard Model in general, we recommend the Particle Adventure.
- What are neutrinos?
- How were neutrinos discovered?
- Where do neutrinos come from?
- How do we detect neutrinos?
- How many kinds of neutrinos are there?
- What is the Solar Neutrino Problem?
- Do neutrinos have mass?
- What are neutrino oscillations?
- How are neutrino oscillations measured?
- What is CP violation?
- What is δ?
What are neutrinos?
Neutrinos are a kind of elementary particle – that is, they are subatomic particles which don’t give any indication of being made of smaller pieces. They are similar to electrons, except that electrons have electric charge –1 (in the units particle physicists use; in SI units that’s –1.6×10-19 coulombs), whereas neutrinos have no electric charge. Neutrinos are also much less massive than electrons – not more than 4 millionths of the electron mass (and the electron itself has a mass only 1/1837 of that of a hydrogen atom).
In the Standard Model of particle physics, matter is made up of two types of elementary particles: hadrons, which feel the strong force that holds protons together in the nucleus, and quarks together in the proton, and leptons, which don’t feel the strong force. Neutrinos, like electrons, are leptons. They are denoted by the symbol ν, which is the Greek letter “nu” or n (it’s not a V, though it may be hard to tell in some fonts!).
Neutrinos should not be confused with neutrons, a constituent of the atomic nucleus, or with neutralinos, hypothetical particles that may explain the dark matter content of the Universe.
How were neutrinos discovered?
The existence of neutrinos was first suspected as a result of the properties of a type of radioactive decay called beta decay, in which an electron – or its antiparticle, a positron – is emitted. It was found that the electron did not carry away all the energy that had been lost by the decaying nucleus. In 1930, Wolfgang Pauli, an Austrian theoretical physicist, suggested that the missing energy must be accounted for by an undetected neutral particle also produced in the decay. A few years later, the Italian-American theoretical physicist Enrico Fermi called Pauli’s particle a neutrino, and the name has stuck.
Neutrinos interact only very weakly with matter, and are consequently very difficult to detect – indeed, Pauli feared they might never be detectable. However, the advent of nuclear reactors after World War II provided physicists with a very intense source of neutrinos, and in 1955 Fred Reines and Clyde Cowan managed to detect neutrinos through so-called inverse beta decay, in which a proton captures an antineutrino (instead of emitting a neutrino): ν + p → n + e+. Reines and Cowan detected the positron when it annihilated with an electron, and the neutron when it was captured by an atomic nucleus. This double signal allowed them to say for sure that they were really seeing neutrinos and not cosmic rays or some other background.
Therefore, 25 years elapsed between the first suggestion that neutrinos should exist and the first unambiguous experimental detection. This is a measure of how difficult experimental neutrino physics really is!
Where do neutrinos come from?
Neutrinos are probably the second most common particle in the Universe, after photons (depending on exactly what dark matter is, they might be the third most common, after photons and dark matter particles). They were produced in huge numbers in the period immediately after the Big Bang: cosmologists calculate that there should be over 300 neutrinos per cubic centimetre everywhere in the entire Universe from this source. (A cubic centimetre is about the size of a sugar cube.) Stars also produce vast numbers of neutrinos: the Sun produces over 60 billion per square centimetre per second at the Earth’s distance. Other astrophysical phenomena, such as supernovae (exploding stars) and cosmic rays, also produce neutrinos.
On Earth, neutrinos are produced naturally by some radioactive isotopes, such as carbon-14 (used for carbon-dating archaeological artefacts) and potassium-40, and also by cosmic rays striking the Earth’s atmosphere. They can also be produced artificially by nuclear reactors and by particle accelerators. The artifical processes are very similar to the natural ones: reactor neutrinos just come from radioactive beta decay, and accelerator neutrinos come from exactly the same process as cosmic-ray neutrinos, just in a more controlled environment.
Fortunately, because neutrinos are so weakly interacting, they are completely harmless: although hundreds of billions of solar neutrinos are passing through you at this very moment (even if it happens to be night-time – they pass through the Earth too, no problem), the chances that one of them will interact with an atom in your body are very slim indeed. Persuading a neutrino to interact makes winning the Lottery look like a very safe bet!
How do we detect neutrinos?
In order for you to detect something, it has to interact with your detector. You can see because photons of light are absorbed by the rod and cone cells of your retina; glass is transparent because photons of light aren’t absorbed by glass. (The Invisible Man of the movies would be blind: his retinas are transparent, so they aren’t absorbing photons.) Neutrinos interact only very weakly, so they are very hard to detect: to be reasonably sure of having a typical solar neutrino interact, you would need to run it through at least a light-year of lead.
Fortunately, interactions are random: you might need a light-year or more of lead to stop all your solar neutrinos, but a few of them will interact in the first inch. (Similarly, it’s possible that the first Lottery ticket you ever buy in your entire life will win the jackpot – it’s just not very likely.) Therefore, if you have a large enough detector and a sufficiently intense beam of neutrinos, enough of them will interact to make the experiment worth doing, even though 99.9999999999% of them go straight through.
Neutrinos interact in two ways:
- they may simply bounce off whatever they hit (electron or atomic nucleus) – the neutrino remains a neutrino, but it transfers momentum and energy to the struck object;
- they may convert into a charged lepton (an electron, muon or tau, or their antiparticles, depending on the type of neutrino). This requires that not only energy and momentum, but also electric charge, be transferred, since the neutrino is electrically neutral but the lepton it converts into is not.
In the first case, we can detect the struck object, usually because it is now moving, occasionally because it has broken up. In the second case, we usually detect the charged lepton, but sometimes we detect the change in the charge of the struck object. There are many ways of detecting a moving charged particle: we can track it as it ionises the material through which it passes, or we can detect the light it will emit if it is traveling at a speed > c/n, where c is the speed of light in a vacuum and n is the refractive index of the (transparent) material through which it is moving. This light is called Cherenkov radiation, after Pavel Cherenkov.
Here are a few examples of each type of detection, with links to experiments that use them:
- Detection of recoil of struck object
- This is used to detect solar neutrinos: an electron is struck by the neutrino, recoils and is detected by its Cherenkov radiation. Example: Super-Kamiokande.
- Detection by break-up of struck object
- This was used by the SNO experiment. The struck object was a nucleus of deuterium, the rare heavy isotope of hydrogen, which contains a neutron in addition to the usual proton. The deuterium nucleus breaks up into its constituent proton and neutron, and the neutron is observed when it is captured by an atomic nucleus (the energy it loses as it binds to the nucleus is emitted as a high-energy photon or gamma-ray, which is then detected).
- Detection of produced charged lepton
- The charged lepton detected is usually an electron, a muon, or their antiparticles: the tau is much harder to produce in the first place, because it is more massive, and much harder to detect because it is very short-lived. An example of an experiment which tracks the charged particle by its ionisation is MINOS or the T2K near detector ND280; an example of a detector that detects the charged particle by its Cherenkov radiation is IceCube or the T2K far detector Super-Kamiokande.
- Detection of charge change in struck object
- This type of experiment is capable of detecting extremely low energy neutrinos. The idea is that the neutrino interacts with an atomic nucleus, and the change in charge changes the atom into a radioactive atom of a different element. You then chemically extract the different element, and count the number of atoms you made by watching their radioactive decays. The method has severe disadvantages – you don’t know which direction the neutrino came from, what energy it had, or exactly when the interaction occurred – but is the only way of detecting neutrinos with energies less than 1 MeV (1.6×10-13 J). An example of this technique is the first detector ever to detect neutrinos from the Sun: the Homestake experiment set up by Ray Davis, in which chlorine-37 is converted into radioactive argon-37.
How many kinds of neutrinos are there?
In the Standard Model of particle physics, there are three kinds of charged lepton: the electron, muon and tau. An experiment done in 1962 by Lederman, Schwartz and Steinberger showed that the neutrino produced in association with the muon could not convert into an electron, and precision measurements of the production of the Z boson confirmed that there were three light neutrinos to match the three charged leptons. The charged leptons all have antiparticles of opposite charge, and the failure of reactor neutrinos (which ought to be electron antineutrinos) to convert chlorine to argon – which solar neutrinos, which are electron neutrinos, can do – suggests that neutrinos and antineutrinos are different, so altogether there would be six distinguishable types of neutrinos.
The current model of neutrino physics does, however, suggest that the difference between neutrinos and antineutrinos might be an illusion: they may interact differently because they spin in opposite directions, not because they are fundamentally distinct. That would cut the number back to three.
On the other hand, some currently inexplicable experimental results may indicate the presence of sterile neutrinos, which interact only via gravity (an extremely weak force on the scale of subatomic particles) and therefore cannot be directly observed by any experiment. The jury is still out, but it is possible that one or two types of sterile neutrinos might turn out to be necessary to explain experimental results, bringing the total number up to four or five. Sterile neutrinos really would be the undetectable particles Pauli worried about, although it is possible that cosmological measurements, e.g. the temperature fluctuations in the cosmic microwave background, might provide indirect evidence.
What is the Solar Neutrino Problem?
When Ray Davis started detecting solar neutrinos with his Homestake experiment, a tank of cleaning fluid (C2Cl4) in which neutrinos can convert occasional atoms of chlorine into argon, he saw only 1/3 of the number he expected. The expected number was based on the Standard Solar Model (SSM) calculations of John Bahcall and co-workers; the SSM describes all the other features of the Sun that we know about, including important ones like the amount of energy it puts out, so there was no obvious reason why it should get the number of neutrinos so wrong – especially as neutrinos are an essential by-product of the Sun’s energy-generating reactions.
As long as only a single experiment observed solar neutrinos, it was possible that the problem might lie with the experiment: perhaps Davis’ method of extracting and counting argon atoms was much less efficient than he believed. However, in the 1980s and 1990s other experiments, namely Kamiokande (predecessor of Super-Kamiokande), GALLEX/GNO and SAGE, also saw fewer solar neutrinos than expected. These experiments used different techniques and were sensitive to neutrinos of different energies, making the idea that it was all the fault of incompetent experimenters untenable. This, then, was the Solar Neutrino Problem: why do all these experiments see fewer neutrinos than expected?
The Solar Neutrino Problem is no longer a problem. All the above experiments could see only electron-type neutrinos. The SNO experiment, which used heavy water, D2O, instead of ordinary water, could see other types of neutrino as well (see How do we detect neutrinos?). In 2002, SNO produced a paper showing that the total number of neutrinos of all types was consistent with the SSM: it was just that, although they were all produced as electron-type neutrinos, by the time they reached Earth some of them had transformed into some other type (SNO could not tell if the “other type” was muon-type, tau-type or a mixture). Therefore, the Solar Neutrino Problem is now resolved, and the resolution is neutrino oscillations.
Do neutrinos have mass?
Pauli originally thought that neutrinos might have a small mass, but later experiments failed to find one, and by the 1960s it was generally assumed that neutrinos had exactly zero mass. The original formulation of the Standard Model of particle physics explicitly assumes that neutrinos have no mass. However, the resolution of the Solar Neutrino Problem – the transformation of electron-type neutrinos into some other type – only works if neutrinos have non-zero masses: massless neutrinos cannot switch identities in this way. Therefore, because of solar neutrinos and a similar effect called the atmospheric neutrino anomaly – a deficit of muon-type neutrinos produced by cosmic rays in the Earth’s atmosphere – we know that neutrinos must have mass. However, we do not know what their masses actually are.
Neutrino oscillations are only sensitive to the differences in neutrino masses (more specifically, the differences in the squares of the masses). They cannot tell us the absolute mass of any type of neutrino. To do that, we have to look at radioactive beta decay, in which an unstable atom decays an emits an electron and an antineutrino (or a positron and a neutrino, depending on the isotope). The electron and the neutrino share the energy released by the decay. If the neutrino has a small mass, Einstein tells us that the minimum possible energy it can have is its mass-energy, E = mνc2. If it has zero mass, it could on very rare occasions carry away no energy at all. Therefore, if we look at the distribution of electron energies very close to the maximum value, we should see a slight change in the expected shape if the neutrino has mass.
This experiment is usually done using the unstable heavy isotope of hydrogen known as tritium, which has two neutrons in addition to its proton. Tritium decays to helium-3 with a half-life of 12.3 years, and the mass difference between helium-3 and tritium is rather small, which makes the tiny distortion caused by a non-zero neutrino mass slightly easier to see. It’s still a very hard experiment, and the best that we have been able to do so far is to prove that the neutrino emitted in beta-decay cannot have a mass of more than 2 eV (4 millionths of the mass of the electron). A new tritium beta-decay experiment under construction in Germany, KATRIN, hopes to reduce this by a factor of 10.
If the neutrino is indeed identical to its antiparticle, as most theorists believe (see How many types of neutrino are there?), greater sensitivity can be achieved using a very rare type of radioactive decay known as double beta decay. In this process, as its name suggests, the isotope emits not one electron but two, decaying not to its nearest neighbour in the Periodic Table but to its next-but-one neighbour. This is a fantastically unlikely process, and the half-lives of isotopes that decay this way are about a billion times longer than the age of the Universe: for all everyday purposes, they are completely stable, and it takes a very sensitive experiment to see them decay at all. (It works the same way as detecting neutrinos: although on average the atoms live for a billion times the age of the universe, there is a very tiny chance that one will decay tomorrow: if you have a large enough detector, and monitor it carefully enough, you will see a few decays.)
The isotope may emit two antineutrinos along with the two electrons – this is a perfectly standard, allowed (if extremely rare) decay process, and it has been measured. However, if the neutrino and antineutrino are really different aspects of the same particle, once in about a million times the neutrino produced in association with one electron may be absorbed in producing the other (it’s got to be an antineutrino in the emission, and a neutrino in the absorption, which is why this only works if the two particles aren’t really different). This is neutrinoless double beta decay, and the (tiny) rate at which it occurs depends on the neutrino mass. Observing such decays allows the experimenters to measure neutrino masses of 0.1 eV or less – about a factor of 20 below the current limit. As yet, there is no convincing detection (one group claims to have seen a signal corresponding to a neutrino mass of about 0.4 eV, but this is not generally accepted by the community – which doesn’t necessarily mean it’s wrong, it just means the evidence isn’t convincing enough), but half-a-dozen or so new experiments are currently under construction or taking data, so this situation may well change in a few years.
What are neutrino oscillations?
We know that there are three types of neutrino, one for each of the three charged leptons. However, we only measure the type, or flavour, of a neutrino when we see it interact, either in association with a charged lepton, e.g. 14C → 14N + e– + νe, or converting into a charged lepton, e.g. νμ + n → p + μ–. When it’s just travelling along not doing anything, we do not have direct evidence of its type. We do, however, in principle know what its mass is: a free particle obeys Einstein’s relation E2 = p2c2 + m2c4, and therefore has a well-defined mass. There are three different neutrino masses, just as there are three different neutrino flavours.
Neutrino oscillations happen if the division of neutrinos into different flavours doesn’t line up with their division into masses. In quantum mechanics, this is perfectly possible: consider Schrödinger’s infamous cat, which is 50% alive and 50% dead until you open the box. We produce the neutrinos in some defined flavour state (which is a mixture of mass states), but as they travel from production to detection the three mass states get out of step, so when we detect them they are no longer perfectly lined up in the original flavour state.
Polarised sunglasses offer an analogy to this. Light is a transverse wave: the electric and magnetic waves wiggle at right angles to the direction of motion, like water waves or waves on a string. In ordinary light, the waves are at all kinds of random angles, but you can describe this as a sum of two components, horizontal and vertical (just as you can describe any square on a chessboard by two numbers, row and column). This is why polarised sunglasses cut out glare so well: direct sunlight is almost a 50:50 mix of the two polarisation states, but light reflected from a horizontal surface is mostly horizontally polarised. So if your sunglasses pick up vertically polarised light, they will cut the intensity of sunlight by about half, but the intensity of reflected light by much more than half.
If you take two pairs of polarised sunglasses, and align them at 90° to each other, you’re cutting out both polarisations. As all light can be decomposed into horizontal and vertical components, you’ve cut out all the light: the two crossed lenses should be practically black.
Now take a third pair of sunglasses, and insert them between the other two at an angle of 45° or so. You should find that, amazingly, the area where all three lenses intersect is much more transparent than it was when there were only the two lenses there! Putting in something that blocks half the light has suddenly let more light through – what’s happened?
The answer is that vertically polarised light can be described as a 50:50 mix of two 45° polarisations arranged in an X shape. Conversely, light polarised at 45° is a 50:50 mix of horizontal and vertical polarisations. Therefore, your tilted glasses take the vertically polarised light from the first pair of sunglasses and pick out only the 45° polarisation (not the 135° polarisation). But this is now a mixture of horizontal and vertical – so the third pair of glasses can pick out a horizontal component which wasn’t there in the pure vertical polarisation after the first pair of glasses. The intensity is cut down quite a bit, of course – if you work through, you’ll see that we’re down to one-eighth of the original light level – but it’s a lot more than zero.
In neutrino oscillation, the distance between production and detection acts a bit like the third polariser: by dividing the neutrinos according to mass instead of flavour, it regenerates a mixed flavour state from the pure flavour state produced in the original interaction. The analogy isn’t perfect: the strength of the effect varies with distance in a sinusoidal fashion (imagine rotating the third polaroid gradually through 360°), and you can get more than 50% conversion between flavours. But it gives the right general idea.
How are neutrino oscillations measured?
Neutrino oscillations can be measured in two ways:
- Disappearance experiments
- You start with a known flux of neutrinos, and count how many you observe at a certain distance from the source. The oscillation signal is a reduction in the observed number compared to what you would expect. The Solar Neutrino Problem is a disappearance experiment.
- Appearance experiments
- You start with a pure beam of neutrinos of some type X, and you attempt to detect neutrinos of type Y. The oscillation signal is successful detection of type Y. T2K is an appearance experiment.
Both experiments can produce misleading results in some circumstances. Disappearance experiments can give a false positive if the flux of neutrinos is smaller than you believe, or if the efficiency of your detector is not as good as you think it is. Appearance experiments can be fooled if the beam is not really 100% pure type X, but contains a small amount of type Y already, or if your experiment is not quite 100% accurate in distinguishing X from Y. Therefore it is good to have a near detector, close to your source, as well as a far detector at your chosen distance. The near detector measures the beam before the neutrinos have had a chance to get out of step, so it tells you what the original flux is and how many type Y neutrinos there are in your supposedly Type X beam. You then compare the near and far detector results to extract the change in flux or the excess of type Y which is your oscillation signal. You also need to understand your detector extremely well, in order to minimise the chance that inefficiencies or misidentifications are affecting your signal.
What is CP violation?
We have long known there are three neutrino “flavours”: electron, muon and tau. From neutrino oscillations experiments, we now know there are three corresponding neutrino mass states, which – with uncharacteristic lack of whimsy, for physicists – we simply call 1, 2 and 3. According to the basic rules of quantum mechanics, each flavour state can be regarded as some mixture of all three mass states, and vice-versa. Therefore, in principle, three independent types of oscillation, or mixing, between mass states are possible: 1 with 2, 2 with 3, and 3 with 1. (As mentioned above, some physicists think there might also be a fourth neutrino flavour, “sterile”, which cannot participate in neutrino oscillations – but it does not enter this discussion.) Each oscillation variety has two associated quantities: the mass difference between the two states involved, and the so-called mixing angle θ. The latter is just a convenient way of ensuring that all quantum mechanical probabilities add up to 100% properly. This “unitarity” requirement is automatically satisfied if we take advantage of the rule from trigonometry, sin2 θ + cos2 θ = 1 for any angle θ. There is no physical “angle” involved in neutrino oscillations: θ is just a parameter that lets us describe the amount of mixing, while guaranteeing unitarity is preserved. If sin2 θ or cos2 θ ~ 0, one mass state dominates; if sin2 θ ~ cos2 θ, the two mass states are about equally represented in the sum (“maximal mixing”).
We know the mixing angles θ12 and θ23 are large, that is, mixing is nearly maximal for these pairs of mass states. However, until recently the best measurements of the third mixing angle θ13 were consistent with zero – only an upper limit on its value could be determined. T2K’s first main goal, now achieved, was to determine if θ13 is actually not zero. Thanks to T2K and the reactor experiments, we now know that it isn’t: the current best estimate is θ13 = 8.5°. The key consequence of having all three angles non-zero is that this allows CP violation in the neutrino system, via a quantity known as δ. So what is CP violation, and why is it important?
The symbols C and P each denote a mathematical operation to be carried out on the description of a physical process. C, charge conjugation, is the replacement of all the particles in the interaction by their antiparticles: the name refers to the fact that in most cases the most obvious sign of this replacement is the reversal of the charge – for example, antielectrons (positrons) have positive charge, and antiprotons have negative charge. (Neutrinos are uncharged, but neutrinos and antineutrinos are distinguished by their helicity, i.e. the direction of their spin.) P, parity, describes mirror reflection: the coordinates (x, y, z) of all particles in the interaction are reversed to (–x, –y, –z), and the directions of any motions are reversed too. In quantum theory, C and P are each represented by a mathematical operator that performs these swaps.
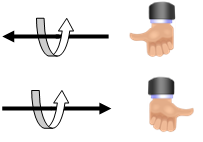
C (or P) is said to be conserved if the interaction after the application of C (or P) looks physically valid and correct. In our everyday world, we don’t get to swap particles and antiparticles very often, but parity conservation seems like a fact of nature: if I showed you some film of a soccer match, a snooker game, or an archery contest, provided there were no advertising slogans visible you would not be able to tell if the film had been reversed left to right – the behaviour of the balls or arrows would seem perfectly natural. And up to the 1950s it was indeed assumed that parity conservation was a law of nature. However, it was then pointed out by Chen Ning Yan and Tsung-Dao Lee that parity might not be conserved in weak interactions, which are not so visible in everyday life. This suggestion was tested in 1956 by an experimental team led by Chien-Shiung Wu, and found to be correct – parity is not conserved in weak interactions. In fact, it is maximally violated: the weak interaction is sensitive to left-handed particles and right-handed antiparticles, and not to their parity-reversed cousins, right-handed particles and left-handed antiparticles (handedness in particles refers to the direction of spin: “right-handed” means that the spin direction is aligned with the direction of motion, as in the figure).
The same weak interactions that violate P also violate C: antiparticles do not behave in the same way as particles (if we only switched particle identity, a left-handed neutrino would become a left-handed antineutrino, which would not feel the weak interaction and so would not behave like a “real”, right-handed, antineutrino). However, the combination CP (switch particles for antiparticles, and mirror-reflect coordinates) works much better, and for a while CP conservation was believed to be a genuine law of nature.
However, in 1964 James Cronin and Val Fitch showed that in some circumstances the weak interaction could also violate the combined CP symmetry. This is a much weaker effect than the violation of C and P separately: it occurs only in certain interactions (Cronin and Fitch were looking at neutral kaons; the effect has since been observed in B mesons as well), and even there only at the 1% level.
CP violation is extremely important, because it represents a genuine difference between particles and antiparticles. One of the unsolved mysteries of cosmology is that our Universe appears to be made entirely of matter, and not a 50:50 mix of matter and antimatter, although when we make particles in the laboratory they always come as particle-antiparticle pairs. Interactions that violate CP are one of the three essential conditions for generating a matter-only Universe that were proposed in 1967 by Andrei Sakharov (the other two are violation of baryon-number conservation, which is obviously necessary to generate a non-zero net baryon number from an originally symmetric, B = 0, state, and departure from thermal equilibrium, which is necessary to ensure that forward-going, baryon-making, processes aren’t balanced by backward-going, baryon-destroying, reverse processes). Therefore, CP violation is essential for our Universe, as we know it, to come into being.
From the viewpoint of a neutrino physicist, the most interesting thing about CP violation in kaons and B-mesons is that it seems to occur at too low a level to give the amount of asymmetry that we observe in our matter-only universe. This is why the observation of a non-zero third mixing angle, and hence the possibility of CP violation in neutrinos, is so important: it may just hold the key to one of the great unsolved mysteries of the cosmos.
What is δ?
The symbol δ is used in the mathematics of neutrino oscillations to describe the part of the oscillation that is CP violating: it causes a change of sign between neutrinos and antineutrinos, and therefore causes them to behave differently in oscillations. Observable CP violation requires there to be three distinct types of oscillation, with three distinct and non-zero mixing angles. This is why the observation of a non-zero value for the third mixing angle θ13 is such an important finding.