3つのニュートリノの質量固有状態(ν1, ν2, ν3)と,3つのフレーバー固有状態(νe, νμ, ντ)の関係は,通常3行3列の行列で表され,提唱者であるブルーノ・ポンテコルボ(Bruno Pontecorvo),牧二郎,中川昌美,坂田昌一の4名にちなんでPNMS行列と呼ばれて います。この行列は3つの混合角と1つの位相角によって以下の形で書かれます。
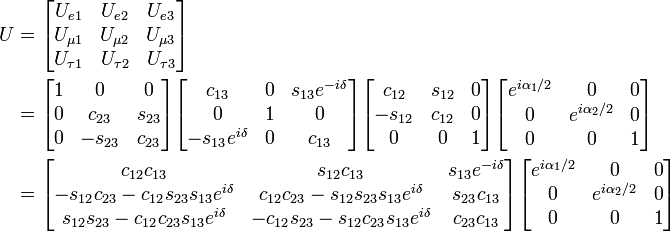
ここで、s12はsin(θ12),c12はcos(θ12),δはCP対称性の破れの位相であり,ここにさらに付け加わっているα1とα2は二重ベータ崩壊などの現象にのみ現れてきます。
このいささか難しそうに見える式で鍵となる特徴は以下のようになります。
- 混合角θ12(太陽ニュートリノ振動)とθ23(大気ニュートリノ振動)は極めて精度よく決められており,その値は大きいことが分かっています。(θ12 = 34°±1°,θ23 > 40°,混合角が取りうる最大値は45°)
- これは予想外のことで,クォークにおいてこれに相当する混合行列(カビボ・小林・益川行列またはCKM行列)では,全ての混合角は極めて小さく,3行3列の行列はほぼ対角的です。
- 3番目の混合角θ13は他の2つと異なり非常に小さく,2011年6月の時点でまだ直接的な測定はなされていません。(文献[10]のように,それまでに得られた全てのデータをフィットすると,θ13が0でない正の有限値でわずかによいフィット結果が得られますが,その効果は小さく,現時点ではあまり説得力がありません。)
- θ13の値がゼロでないことは,CP対称性を破る位相δを観測するためには必要不可欠です。
Δm122 << Δm232であるので,どちらの質量階層構造が正しいかに関らず,Δm232とΔm132の差は小さくなります。このことは,θ13 の効果を最大にするのに適したL/Eの値はθ13 よりもはるかに大きいθ23に対しても同じようにあてはまることを意味しています。大気ニュートリノ振動は,電子ニュートリノではなくミューニュートリノが関与するので,これは主にT2KやMINOSのような加速器を使用したニュートリノ振動実験の対象になります。また,原子炉を利用した実験で使われるのは電子ニュートリノビームであるので,それぞれに関係する質量差Δm122とΔm232はよく分離しており,どちらを選んで調べるかでL/Eを最適な値に調整することができます。
振動実験の基本的事項
ニュートリノを検出するという目的に合わせて設計されニュートリノ振動現象を実際に発見したこれまでの実験とは異なり,ニュートリノ振動実験は,特にニュートリノのフレーバーが飛行中にどのように変化するかを研究するように設計されています。これには2つの基本的な方法があります。
- 消失実験:特定の種類のニュートリノを生成し,しかも生成されたニュートリノの個数が分かっている場合に,距離Lだけ離れたところで検出される同じ種類のニュートリノの数を数えます。観測された数が少なければ,それは振動が起こった信号です。
- 出現実験:ある1種類のニュートリノを生成し,それとは異なる種類のニュートリノを観測する場合を考えます。全ての背景事象を考慮した後で,この異なる種類のニュートリノの個数がゼロでなかった場合,それは振動が起こった信号になります。
原子炉ニュートリノ実験では常に消失実験が行われます。なぜなら,原子炉ニュートリノのエネルギーは典型的に数メガ電子ボルトで,これは異なる種類のニュートリノを生成するのに十分ではないからです。低エネルギーニュートリノで“出現”実験を行う唯一の方法は,太陽ニュートリノ検出を行うSNO実験のように,中性カレント反応と荷電カレント反応との直接比較を行うことです。これは素晴らしい実験でしたが,大量の重水が使用できる条件が必要です。(SNOは特別なケースでした。) したがって,消失実験が唯一の現実的な選択になります。
消失実験で鍵となる点は,以下の2つを正確に理解することです。1つ目は検出器に入ってくるニュートリノフラックス(明らかに,どれだけ消失したかを求めるには最初にどれだけの数が期待されるかを知っている必要があります。)で,2つ目は事象の検出効率(もしこの算出が正確でないと,実際はニュートリノが存在したにも関わらずそれらを見逃してしまい,ニュートリノが消失したと考えてしまうかもしれません。)です。原子炉からのフラックスの計算は非常に困難(前述の人工ニュートリノ発生源を参照)で,これは実際にいくつかの原子炉実験における制限要因となってきました。も し,実験がChooz実験のように特定の1つの原子炉からのニュートリノを調べるように設計されているのならば,同型の2つの検出器を建設してニュートリノフラックスをモニターすることが出来ます。1つを原子炉の近くに建設して(前置検出器)ニュートリノが振動を起こす前のフラックスを測定し, もう1つを遠方に建設して(後置検出器)同じようにフラックスを測定します。両者の信号の比をとることで,全体のフラックスおよび(前置と後置の検出器が同じデザインであれば)検出効率の不定性の多くを相殺できます。カムランド実験のように多くの原子炉からの複合フラックスを検出する場合,これはそう簡単ではありません。この場合,データの統計量が十分であれば観測されたフラックスの変化と原子炉の電力出力記録の相関を見ることでいくつかの確認を行うことができますが,前置検出器はあまり役に立ちません。
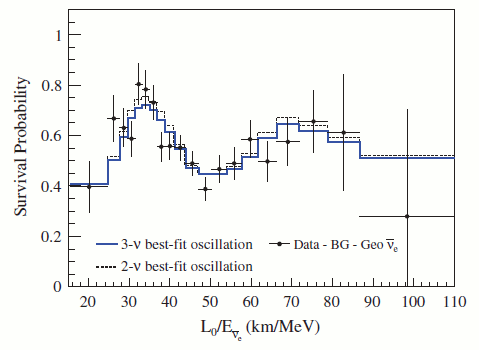
図18:KamLAND原子炉ニュートリノ実験で得られた振動。プロットは残存確率がどのように変化するかをL/Eの関数で示している。点は(既知のバックグラウンドを差し引いた)データ,線は振動モデルからの予測である。A. Gando et al., Phys. Rev. D83 (2011) 052002から引用。
原子炉ニュートリノは非常に大きなエネルギーの広がりを持つので,ある決まった距離Lに置かれた検出器は,実は振動の方程式にでてくるL/Eに関してある範囲における何通りもの組合せとして事象を記録しています。このことは,もし検出器が高いエネルギー分解能を持つならば,期待される sin2(1.267 Δm2 L/E) の振る舞いを探すことで本当に振動現象を見ているのかどうかを確認することができます。図18はカムランド実験によって得られたそのようなプロットです。これは信号が本当に振動からのものであるという重要な確認になります。もし,計算されたフラックスの間違いや事象を再構成するときに予想外の問題によって引き起こされたものであるならば,このように綺麗なサイン波のパターンを見ることはないでしょう。
出現実験は,出現という肯定的な結果に反論の余地は無いという点で消失実験よりも明解だと言えます。もしビームが純粋なタイプXのニュートリノの場合にタイプYのニュートリノを検出したとすると,そこでは明らかに何かが起こっています。しかし実際には判別はそれほど明確ではありません。加速器で生成されたミューニュートリノビームは100%純粋ではなく,検出器での粒子識別は100%の効率ではないからです。(ビームは常にいくらかの電子ニュートリノを含んでおり,検出器でもタイプXの事象を検出してもそれをタイプYと間違えたり,XでもYでもないただのバックグラウンドをタイプYと識別してしまったりすることがあります。)このことから出現実験に対してデザイン的に重要な事項が出てきます。それは,まずもともとある他のフレーバーからの混入を正確に見積り,ビームをよく理解しておく必要があります。さらによく理解されていて高い粒子識別能を持つ検出器を持ち,起こりうるバックグラウンド過程を全てよく知っておくことが必要になります。
ビームの特性を知るために前置検出器が必要になります。ニュートリノが振動する前にビームの測定を行い,これらの結果を後置検出器からの結果と比較します。もし,前置検出器と後置検出器が非常に似ていれば(前置検出器は高いフラックスに対応するためにおそらく小さくすることになりますが),前置検出器と後置検出器で得られた結果を比較することによって,消失実験と同じように,検出器の効果をいくらか相殺できます。これはMINOS実験で取られたアプローチです。MINOSの主目的は消失実験ですが,νe出現を探索するためにもデザインされています。
T2K実験においては,前置検出器は現在世界中で品質のよいデータサンプルが得られない様々なニュートリノ反応の測定を行うことによって,起こりうるバックグラウンド過程の理解をより深めるという役割を負っています。重要な例は荷電カレント反応νμ + p/n → νμ + p/n + π0 での中性パイ中間子π0の生成です。π0は2個の光子に崩壊します。水チェレンコフ検出器において光子はほとんど電子と同じに見えます。したがって,もし光子の1つが非常に低いエネルギーのために検出されなかった場合には,その事象を電子ニュートリノ荷電カレント反応と容易に間違ってしまうでしょう。このために,そしてまた加速器に非常に近く置かれているため期待される事象数が多くなるので,T2K前置検出器ND280は水チェレンコフ検出器ではなく飛跡検出器になっています。前置検出器と後置検出器で異なる検出効率を計算する必要があるという不利な点があるものの,このアプローチの有利さがそれを上回ると期待されています。
実は,加速器で生成されたミューニュートリノビームを用いた出現実験は常に消失実験でもあります。なぜなら,Δm232とΔm132は非常に近いので,νe出現事象を探索してθ13を測定するようにデザインされた実験は,νμ消失にも感度があり,出現実験に必要な検出器デザイン(ビームへの他のフレーバーの混入を測定する前置検出器,高い電子-ミューオン識別能力および高いバックグラウンド除去能力)はまた消失事象の測定に非常に適しています。(前置検出器は振動する前のミューニュートリノフラックスを測定し,また高い粒子識別能力や高いバックグラウンド除去能力は消失事象の解析に有用です。)
消失実験の例として,Double Chooz(Chooz実験を引き継いだ原子炉実験),カムランドがあります。
出現実験の例としては,MINOS, T2K, OPERA(タウニュートリノ出現), ICARUS(多目的の液体アルゴン飛跡検出器),MiniBooNEがあります。
3成分ニュートリノ振動
2011年3月の時点で得られていた全データのグローバルフィット[10]を表1に示しました。このフィットに使われたデータのうちどれも θ13 > 0 の直接的な証拠を与えてはいませんが,異なる2成分ニュートリノ振動の結果のわずかな不一致が,フィット結果において θ13 > 0 の傾向を生じさせています。2011年6月にT2K実験グループによって報告された結果はこの値と矛盾ありません。
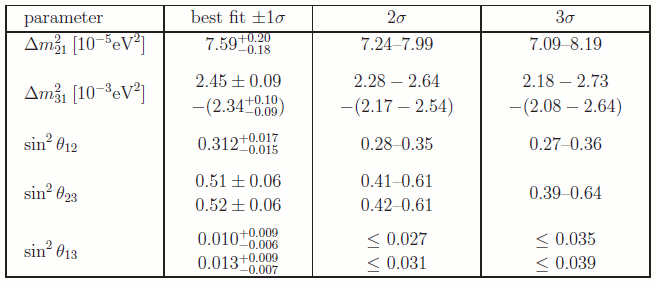
表1:参考文献10から引用した振動実験のグローバルフィットの結果。2つの数が与えられているところは,上段が順階層(m3 > m2 > m1)に対応し,下段が逆階層(m2 > m1 > m3)に対応している。3番目の質量差はΔm322 = Δm312 – Δm212で与えられる。もしフィットでの仮定が正しければ,真値が1番目の列で与えられた範囲(1σ)にある確率は68%,2番目の列で与えられた範囲では95%,3番目の列で与えられた範囲では99.7%。
小さいがゼロではない質量とフレーバー間の大きな混合を持つという3成分ニュートリノの“ほぼ標準模型的”描像においてこれが現状です。ここから興味深い疑問が湧いてきます。まずθ12とθ23がθ13に比べて(さらには標準模型のクォークセクターの混合角に比べて)どうしてそれほど大きいのか分からないとういうことです。さらに,どちらの質量階層が正しいのかも分からなければ,角度δに関しては何も分かりません。(しかし,θ13が我々の考えていたよりも大きいので,次世代の振動実験ではδを測定できるかもしれません。)またニュートリノと反ニュートリノが同じ粒子なのか違う粒子なのかも分かりません。これだけでも,ニュートリノ物理は今後何年もの間興味深い分野になるでしょう。しかし,このフィットに含まれていないいくつかの結果が,ニュートリノに関してさらに多くの驚きをもたらすかもしれません。
3種類のフレーバー振動を超えて:LSND, MiniBooNEと4番目の質量の謎
標準模型は全て3種類,すなわち3種類の電荷+2/3のクォーク,3種類の電荷-1/3のクォーク,3種類の荷電レプトン,3種類のニュートリノがあります。4世代目のクォークとレプトンも,もしそれらが非常に重いために現在の加速器では検出できないのであれば,もちろんあり得ます。しかし,4世代目の軽いニュートリノは確かに無いことが分かっているので,もし4世代目があるとすれば,それは我々が知っている3種類のニュートリノと全く異なるものです。
3種類のニュートリノでは,独立な質量差は2つしかありません。3番目の質量差は他の2つの和になるはずです。(もしジョーがアリスよりも2歳年上で,アリスがキムよりも3歳年上としたら,ジョーはキムよりも5歳年上だと分かるのと同じです。)太陽ニュートリノ振動と大気ニュートリノ振動がはっきりと異なる質量差を示すので,上で議論した振動測定においては全て3種類のニュートリノを考慮しました。
残念ながら,何年もの間もう1つの実験から得られた説明できていない結果があります。その実験は,静止パイ中間子の崩壊で生成されるνμを用いて νμ → νe を探索するLSNDという短基線(L=30m)振動実験です。静止したπ+の崩壊からはμ+とνμが生成され,引き続き(ほとんど静止した)ミューオンからはνeとνμが生成されます。したがって,生成されるニュートリノは電子タイプとミュータイプの両方が混ざっていますが,反ニュートリノは純粋なミュータイプです。したがって,逆ベータ崩壊 νe + p → e+ + n を探索することによって,反電子ニュートリノの出現事象に感度を持ちます。低いエネルギーのビームを用いるので,短基線ということはLSNDがかなり小さなL/Eの値を持っており,太陽ニュートリノ振動や大気ニュートリノ振動で観測される値よりもずっと高いΔm2に感度を持っていることを意味します。それにも関らず,この実験は計算されるバックグラウンド以上に逆ベータ崩壊の大きな超過を観測したのです。その超過は質量の2乗差が0.05 eV2 ~ 100 eV2 に対応する信号に一致しており,またそれは表1に示した太陽ニュートリノ振動や大気ニュートリノ振動からの質量の2乗差とは極めて矛盾するものです。
静止パイ中間子からのニュートリノを使うまた別の実験のKARMENからはニュートリノ振動の証拠は得られませんでした。KARMEN実験の基線長はやや短い(17m)ので,この結果からLSNDの結果を完全に反証することはできませんが,Δm2の許容領域を0.05 eV2 ~ 1 eV2(まだ太陽ニュートリノと大気ニュートリノの結果と矛盾),もしくは他の短基線実験の結果を考慮すると0.2 eV2 ~ 1 eV2 にの範囲に縮めることはできます。これらの結果が2000年ごろに初めて報告されたとき,ニュートリノ物理学コミュニティの一般的な反応は,異常を示す1つの結果だけでは標準模型を大きく変更する十分な根拠にならないというもので,その後10年間は概してLSNDの結果を(おそらく何か想定外のバックグラウンドのために)おそらく間違っているのだとして無視する傾向にありました。LSNDの信号領域を調査するために設計されたL/Eの値を持つ従来型の加速器実験であるMiniBooNE実験が2007年にνμ→νe振動の証拠を得られなかったときに,その傾向はさらに強まりました。(図19を参照)
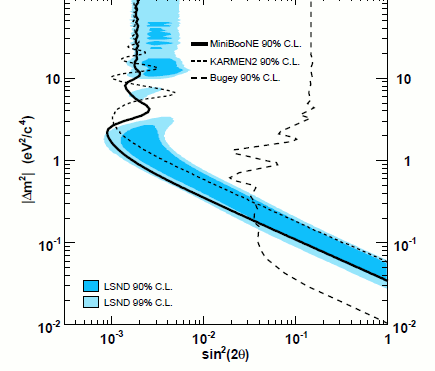
図19:MiniBooNEのニュートリノ振動の結果を他の実験と比較したもの。このプロットでは,太い黒いラインの右側の領域はMiniBooNEによって棄却された領域で,他のラインの右側はKARMENおよび原子炉実験Bugeyによって棄却された領域である。色が付けられた領域はLSNDによって許容される領域を示す。MiniBooNEの結果はLSNDに許容される領域をほぼ完全に棄却している。LSNDの許容範囲の縁に非常に小さなオーバーラップ領域があるものの,全体としてLSNDの結果は98%の信頼水準で棄却される。(LSNDの結果が本物である確率が1/50。)
MiniBooNEはニュートリノを用いましが,LSNDとKARMENは反ニュートリノに感度がありました。このわずかな違いを除くたに,MiniBooNEは引き続いて反ニュートリノビームでデータを収集しました。(反ニュートリノビームはビームパイプ中のホーン電磁石の収束をπ–の替わりにπ+を集めるように設定することで得られます。)皆が非常に驚いたことに,そのデータは比較的低い統計のために大きな誤差棒が付いていたものの超過を観測し,しかしもともとのLSNDの結果に全く矛盾しませんでした。額面通りに取れば,このことは次のことを示唆します。
- 質量2乗差が約0.2 ~1 eV2で,混合角が0.001 < sin2 2θ < 0.03 のνμ とνeの間の混合に対応する振動の信号がある。
- ニュートリノは,反ニュートリノと異なる振る舞いをし,そのような振動はしない。
加えて,MiniBooNEのニュートリノデータは低いエネルギーで電子らしい事象の超過を示しており,これはLSNDの信号と矛盾し,またどんな振動描像とも矛盾しています。しかし,既知のバックグラウンドでは説明できないものです。一方,反ニュートリノにはそのような超過があることを検証または反証できるほど十分な統計がありません。
この超過を検証するためには明らかにもっと多くの統計が必要ですが,反ニュートリノセクターでのMiniBooNEとLSNDの明らかな一致は何かがおこっていて,その何かは標準的な3成分ニュートリノモデルに組み入れることができないことを示唆しています。それでは,どうして我々は既知の3種類のニュートリノと似た4番目のニュートリノが答えではないと確かに言えるのでしょうか? そして他にどんな可能性があるのでしょうか?
ニュートリノの種類の数
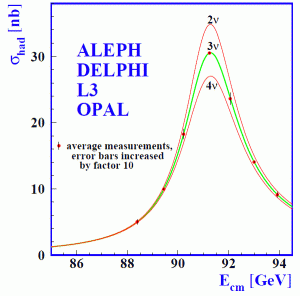
図20:Zボソンのプロファイル。プロットはZボソン生成断面積(基本的にZボソンが生成された数)をLEPのビームの全エネルギーの関数で示している。Zボソンが生成される確率は全エネルギーがZボソンの質量に一致した時に非常に大きくなり,このエネルギースキャンによってZボソンの崩壊幅を決めることができる。ここに示したデータはLEPの4実験全てを併せた全データセットを示しており,線はニュートリノの異なる種類が2,3,4の各場合の期待値をつないだものである。図はPhys. Rept. 427 (2006) 257-454 から引用。
ニュートリノは弱い相互作用で反応します。それは弱い力の伝播粒子であるW±ボソンとZボソンはW+ → l+ + νl (l はe, μ,τ),W– → l– + νl,Z → νl + νl によってニュートリノに崩壊できることを意味します。ニュートリノの異なるタイプの数が多いほど,WボソンとZボソンは多くの行き先に崩壊できるので,その平均寿命は短くなります。量子力学において,不確定性原理は時間とエネルギーを関係付けるので,粒子の寿命はその質量に関係します。つまり,寿命が短いほど質量の不定性(崩壊幅)は大きくなります。したがって,Zボソンの崩壊幅を測定すれば,崩壊先にはいくつの異なるニュートリノのタイプがあるかを決めることができます。この測定はCERNのLHCの前身であるLEPコライダーで行われました。LEPでは電子と陽電子を衝突させました。Zボソンはe+e–に崩壊できるので,もし電子と陽電子のビームの全エネルギーを mZc2 に等しくすれば,LEPのようなコライダーでは大量のZボソンが生成され,Zボソンの崩壊幅を高い精度で測定することができます。結果は図20に示した通りで,3種類のニュートリノによく一致しており,2や4の可能性は確実に排除できます。したがって,もし余りに重くて現在の実験では発見できないような第4世代の標準模型物質粒子があるとすれば,それはZボソンの崩壊で生成されるほど軽くはないと言えます。LSND/MiniBooNEの振動の信号を説明できるほど軽いニュートリノが無いのは明らかです。
ステライルニュートリノ
したがって,3つの異なる相関のない質量の2乗差を説明するためには4種類のニュートリノが必要ですが,Zボソンの崩壊幅を説明するためには4種類の標準模型ニュートリノは不可能です。このことからLSNDの結果が必ず間違いだと言いきれるのでしょうか?
答えはNoです。それは,Zボソンの幅を測定する実験はZボソンに崩壊できるニュートリノだけを数えているからです。もし,弱い相互作用を感じないニュートリノ-例えば右巻きニュートリノ-が存在すれば,それらはZボソンの崩壊幅における種類数のカウントには含まれません。しかし,3種類の既知のニュートリノと混合することはできるでしょう。そのような粒子をステライルニュートリノと呼んでいます。
もともとの標準模型の定式化では質量のないニュートリノを要請しましたが,ニュートリノの質量を含めるだけでは単にニュートリノを他の標準模型粒子と同列に扱うに過ぎないと反論を受けるかもしれません。それゆえに本当の意味での“標準模型を超える”物理ではありません。しかし,ステライルニュートリノは明らかに“標準模型を超えて”おり,したがってそれらが持つであろう性質や振る舞いに関する予言はありません。我々にできることは,すでにあるデータを使ってその粒子が必要とする性質を推察し,それを確認するために将来の実験のデザインを試みるだけです。
ステライルニュートリノを支持する根拠
- LSNDとMiniBooNEの反ニュートリノデータ。
- もしかすると,一般的な原子炉ニュートリノデータ。原子炉反ニュートリノフラックスの最近の再計算によると,これまで考えられていたよりも3%大きいはずであることが示唆されています。もしこれが本当だとすると,原子炉フラックスのこれまでの計算で一致していた全ての原子炉ニュートリノ実験は,実は3%の小さな欠損を測定していたことになります。これはステライルニュートリノへの振動によって説明される可能性があります。
- 宇宙マイクロ波背景放射(CMB)に関するWMAPのデータ。ゼロでない質量のニュートリノはステライルであっても宇宙のエネルギー密度に寄与するので,CMBの構造に影響を与えます。初期宇宙では数eVスケールの質量のニュートリノは光速に近い速度で運動するので,それらは“物質”(つまり陽子や電子,暗黒物質)よりはもっと“放射”(つまり光子)のように振る舞います。WMAPチームが彼らのデータを有効なニュートリノの種類の数をフリーパラメーターとして含むモデルでフィットしたところ4.34±0.87が得られました。このことは3よりは4(または5)の方がやや一致するように見えます。(ニュートリノの種類数の制限はビッグバン元素合成からも得られますが,その計算結果(例えば参考文献[11])からは一般的にニュートリノの種類の数が3か4かを決めることはできません。5には矛盾します。)
- もしかすると,MiniBooNEのニュートリノデータに見える低いエネルギーでの超過。(これは振動の信号のようには見えませんが,ステライルニュートリノモデルがその説明を与えるとすれば,それは有利な根拠になるでしょう。)
ステライルニュートリノに反する根拠
- 太陽ニュートリノ振動に関するKamLAND(反ニュートリノ)とSNO(ニュートリノ)の結果の一致。LSNDの結果は反電子ニュートリノが反ミューニュートリノに振動することを要請します。よって,このセクターにステライルニュートリノを含めようとする場合,すでにずっとよく確立されている太陽ニュートリノ振動データのフィットを悪くしてしまうのを避ける必要があります。
- MiniBooNEのニュートリノデータ。(これはLSNDの振動と矛盾します。上記を参照。)
- “大気”ニュートリノ振動(θ23)に対するMINOSのデータ。そこでは中性カレント反応に欠損がないことを示しています。(つまり,SNOデータと同じように,ニュートリノは存在するがもともとのタイプではなくなっていることを示しています。)もしMINOSのミューニュートリノのうちのいくらかがステライルニュートリノに振動しているとすれば,荷電カレント事象における消失信号(MINOSはもちろん観測しています)と同じように中性カレント事象の数に欠損を観測することが期待されます。
- 全てのタイプのニュートリノの全質量に対して0.58 eVというWMAPが得た上限値。(これは弱い相互作用ではなく重力相互作用に支配されるので,どんなステライルの種類も含んでいます。)これは標準模型の3種類のニュートリノ以上に重いステライルニュートリノを提供することができます(順階層では,例えばLSNDで得られた0.25 eV2の質量2乗差を仮定して0.001 eV, 0.009 eV, 0.05eV, 0.5 eVといった場合が可能)が,もしステライルニュートリノが1つよりも多いとかなり不自然になります。しかし,前述したようにこれは前提としている宇宙論モデルにいくつかの仮定を入れているので,この制限はおそらく省いてもいいかもしれません。
これら全ての制限を同時に満たそうとすることは非常に困難です。1つよりは2つのタイプのステライルニュートリノを導入した方が,振動データは良いフィットを得やすくなります。しかし,これは逆に元素合成のデータと食い違いを生じます。元素合成では1つ余分なタイプを入れるとやや一致がよくなりますが,明らかに2つではありません。その一方で,初期宇宙ではステライルニュートリノが標準模型ニュートリノほど膨大には作られなかった可能性もあります。その場合はおそらくこれは深刻な問題ではありません。MiniBooNEのにニュートリノデータと反ニュートリノデータの間の違いを説明するためには,おそらく非常に多くのCP対称性の破れが必要ですが,これは良いことかもしれません。なぜなら,宇宙の物質と反物質の間の非対称性を作るにはCPを破る相互作用が必要だからです。ステライルニュートリノは標準模型の枠外にあり,しかも超対称性のような“標準的な”標準模型を超える現象とはあまり強い関連性がないので,理論家は現時点ではかなり自由に考えを巡らせることができます。そこにはいろいろな異なるシナリオが含まれ,例えば3+1モデル(ステライルニュートリノが最も重い状態)や1+3モデル(ステライルは最も軽い),3+2, 2+3, 1+3+1の各種モデル(2つのステライルニュートリノがあり,比較的両方が重い場合,両方とも軽い場合,1つが軽くて1つが重い場合),崩壊するステライルニュートリノ,その他諸々です。宇宙論および振動の両方のデータがこの問題を解決するために必要なのは明らかです。Planck衛星が宇宙論の最先端の助けになるでしょうし,SNO+のような新たな太陽/原子炉ニュートリノ振動実験が振動の側に有用な制限を与えてくれることでしょう。



