The T2K Experiment

標準模型のオリジナルの形式化におけるニュートリノの位置付けは以下のようにまとめられます。

それぞれの荷電レプトンに対応する3種類の異なるニュートリノと3種類の反ニュートリノが存在する。
全てのニュートリノは質量がゼロで左巻き（反ニュートリノは右巻き）である。
レプトン数（全レプトンの数から全反レプトンの数を引いたもの）がe, μ, τの3つの世代で独立して保存するように，ニュートリノは対応する荷電レプトンにのみ転換することができ，その逆もまた同様である。

標準模型の発展から何十年が経った現在，すでに確立されたと信じられてきたこれらの性質の基礎が非常に揺らいできました。標準模型の残りの部分は最初から本質的に変わっていませんが，ニュートリノの部分は完全に考え直す必要が出てきました。この動機となったのが太陽ニュートリノ問題と大気ニュートリノ異常でした。

太陽ニュートリノ問題

今になって考えてみれば，ニュートリノの標準模型描像が作られる以前から，その土台に入った亀裂はすでに見えていました。レイ・デービス(Ray Davis)による塩素37を使ったニュートリノ実験の結果から，太陽からやってくる電子ニュートリノのフラックス（流束）が標準太陽模型の予言から期待される数の1/3しか無いことが示されました。当時は太陽模型の信頼性を評価する専門的知識が素粒子物理学者にはなく，この問題があまり深刻に捉えられることはありませんでした。（天文物理学者はニュートリノに問題があると主張し，素粒子物理学者は天文物理学に問題があると主張する傾向がありました。）しかし，1980年代後期に，欠損が本当にあることがカミオカンデII実験によって検証され，そこでは高エネルギー太陽ニュートリノ（>9.3MeV）のフラックスが期待される量の46(±15)%しか観測されませんでした。数年後にはGALLEXおよびSAGEガリウム実験が，0.233MeVより高いエネルギーのニュートリノを標準太陽模型の予測よりも少ない約62(±10)%しか観測できず，欠損の結果は補強されました。弾性散乱では散乱後も粒子の到来方向の情報をいくらか保つため，カミオカンデII実験はそのニュートリノが本当に太陽から来ていることを示すことができました。GALLEXやSAGE実験では人工放射線源を使って検出効率を校正しました。

したがって，1990年中頃までには太陽ニュートリノ問題は現実問題になりました。観測結果を説明しようとする理論家が直面した困難は以下のようなものです。

全ての実験で予測よりも少ないニュートリノを観測している。
しかし，異なる実験では異なる欠損が見られる。（図10を参照）
同じニュートリノに感度がある別々の実験（例えば，GALLEXとSAGE）では結果は一致しており，違いは本物であることを示唆している。
欠損がエネルギーの関数であるとすると，それは単純なものではない。水チェレンコフ検出器実験（高い閾値）とガリウムを使った実験（低い閾値）は両方とも塩素を使った実験（中間の閾値）よりも多くのニュートリノを観測している。

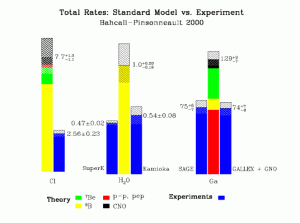
solar neutrino rates - observation and theory

図10：2000年現在における太陽ニュートリノ問題。青い棒グラフは測定値，斜線の領域は実験誤差を表し，中央の色分けされた棒グラフは標準太陽模型を誤差とともに表している。それぞれの色は説明の通り，異なるタイプのニュートリノを表している。ニュートリノ反応確率はエネルギーに依存するので，それぞれの過程からのニュートリノ検出数の期待値は，それぞれの過程で生成されたニュートリノの数に厳密には比例していないことに注意。図はジョン・バコール(John Bahcall)の論文から引用。

理論的にデータを説明しようとすると，これらの特徴を再現する必要があります。

まず，候補となる説明は大きく2つに分けられます。1つは太陽模型に何か誤りがあるとするもので，もう1つはニュートリノの理論に何か誤りがあるとするものです。

太陽模型に何か誤りがある場合: ガリウムを使った実験の結果は，ppニュートリノは大体正しい割合で生成されているが，Be-7ニュートリノが欠けているという考え方におおよそ一致していました。Be-7ニュートリノは，pp-I連鎖反応よりももっと強い温度依存性があるpp-II連鎖反応（図5を参照）から出てきます。したがって，おそらく太陽のコアの温度を少し大きく見積り過ぎていて，実際はpp-II連鎖反応が抑えられていると考えることができます。もしBe-7ニュートリノが欠けているのであれば，塩素を使った実験の結果と水チェレンコフ検出器実験の結果もまた，ニュートリノフラックスの観測期待値と実際に観測されている数の割合に関して矛盾していないことになります。; この考え方の問題点は，図5で見られるようにベリリウム7からホウ素8が作られることです。pp-II連鎖反応を起こさずにpp-III連鎖反応を起こすことはできないにも関らず，ホウ素8ニュートリノはいくらか存在しないといけないので，pp-III連鎖反応は必要です。（そうでなければ，カミオカンデでは何も信号を観測しないことになってしまいます。）この根拠はその当時に得られた広い範囲で独立に計算された太陽模型によって支持されており，その全ての計算においてB-8ニュートリノとBe-7ニュートリノは強く相関することが予測されていました。
ニュートリノに何か誤りがある場合: デービスの実験結果に基づいて最初に推測されたことは，生成されたニュートリノのフレーバーが何らかの理由で太陽と地球の間でランダム化されてしまい，その結果観測されるフラックスが1/3に減ってしまうというものです。（デービスは電子ニュートリノしか観測できなかったからです。）しかし，他の実験では予想される数の1/3よりも明らかに多くのニュートリノを観測したので，この考えは単純すぎるということが分かりました。明らかに，もっと複雑な解が必要でした。

したがって，1990年代中頃までには，標準太陽模型が太陽ニュートリノ問題の答えではないようだと考えられるようになりました。ニュートリノの性質であるニュートリノ振動を使ってそれを説明するために要する数学的技術は，ブルーノ・ポンテコルボ(Bruno Pontecorvo)によって1957年というかなり前に考案されており，振動現象を使った問題の解決策が早くも1980年に物理学のジャーナルに掲載され始めました。しかし当時の素粒子物理学界の大半は，太陽ニュートリノ問題をニュートリノ物理の不明瞭な隅っこの問題として捉えており，理解し難くおそらく信用できないと考えていました。そのような訳で，ニュートリノ振動を明らかに示すものとして観測された証拠は，別のところから出てきました。

大気ニュートリノ異常

その一方で，様々な実験が世界中で大気ニュートリノの測定を始めました。これらはもともと陽子崩壊実験に現れるバックグラウンドを測定することを目的として始められました。前述したように，大気ニュートリノは宇宙線が地球の大気と衝突して生成され，それらにはミューニュートリノが電子ニュートリノに対して2:1もしくはもう少し多い割合で含まれるはずです。しかし通常は，実験でミューオンを検出し同定する効率は，電子に対する効率と異なるので，ほとんどの実験では測定結果を（ミューオン：電子の観測値の比）／（ミューオン：電子の予測値の比）という二重比で報告しています。ここで“予測値の比”は，検出器応答のシミュレーションを行って作った疑似イベントに対し，実データと同じ全ての実験解析過程を通したあとの数値が見積もられます。もし観測値が予測値と一致していれば，この比は実験誤差の範囲で1になるはずです。

図11：大気ニュートリノ異常に関する結果を集めたもの。（参考文献6より）

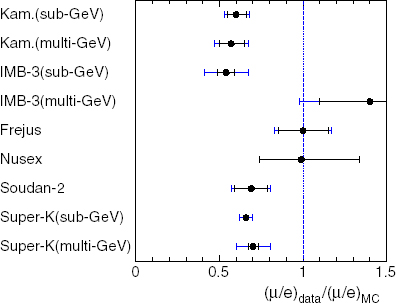
早くからいくつかのヒントはありましたが，有用な結果は1980年代の終わりから1990年代の始めに報告され始めました。最初は，図11に示したように問題のある結果が出てきました。水チェレンコフ検出器（カミオカンデとIMB）は異常に低い二重比を観測し，ミューニュートリノの大きな欠損を示したのに対し，飛跡検出型カロリーメータ（Fréjus, NUSEX）では食い違いが見られませんでした。結果の違いは検出器のタイプと関係しているように見えたので，何らかの系統誤差が含まれているのだと考えられました。幸運なことに，1994年までに飛跡検出型カロリーメータのSudan-2が水チェレンコフ検出器と一致した結果を報告し，ミューニュートリノ欠損が本当であるということに信頼性を与えました。

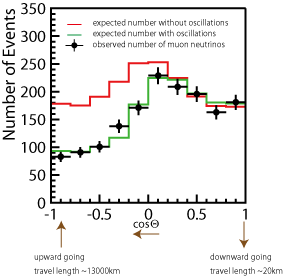
zenith angle distribution for muon neutrinos from SuperK

図12：スーパーカミオカンデから得られた典型的な天頂角分布。期待値（赤いライン）に対して欠損しているデータの量は飛行距離が長くなるとともに増加している。

1998年，スーパーカミオカンデはいくつかの異なるサブサンプル（sub-GeV, multi-GeV, fully-contained, stopping, through-going）を使って詳細な研究結果を公表しました。これらの結果の中で衝撃的だったのは，図12に示したようにミューニュートリノの天頂角分布でした。ここでは欠損が上向きミューオンサンプル，つまりニュートリノが検出される前に地球を貫通してきたものに対して起こっています。これは地球内部での吸収によって起こったものではありません。このエネルギーのニュートリノの反応確率は余りに小さいので問題にならず，また電子ニュートリノに対してはそのような欠損は見られなかったのです。しかし，もしニュートリノがあるフレーバーから他のフレーバーに振動しているならば，ミューニュートリノとして生成されたニュートリノがミューニュートリノとして観測される確率はニュートリノの飛行距離に依存します。この図では，ミューニュートリノの数は天頂角が90度より大きいところで少なくなっています。これらのニュートリノはより長い距離を飛行してきたからです。このモデルで予想される分布を示した緑の線はデータと非常によく合っています。同じように全てのサブサンプルに対しても同様の結果が得られています。（例えば，参考文献[6]の図14は8通りのカテゴリーに分けられたミューニュートリノの天頂角分布を示していますが，全てニュートリノ振動が起こったとした場合によく一致しています。）

素粒子物理学界のほとんどの人々は，それ以前の太陽ニュートリノ観測の長い歴史があるにも関らず，スーパーカミオカンデの結果の発表をニュートリノ振動の“発見”と位置づけています。電子ニュートリノサンプルに何も超過が見られないことから，観測された振動はν_μ → ν_eではないことを示していました。スーパーカミオカンデグループは，最も良い解釈はν_μ → ν_τの振動が起こっていて，タウレプトンの重い質量と短寿命のためにタウニュートリノが観測されないのだと結論しました。

解明 – ニュートリノ振動

それではこれらニュートリノ振動とは何なのでしょうか？　これらの現象が存在するとどうなるのでしょうか？

振動現象の背後にある根本的な考えは，混合状態の量子力学的概念です。最もよく知られている例はシュレーディンガーの有名な猫です。量子力学では，猫が生きている確率が50%で死んでいる確率が50%であるならば，それを観測するまでは2つの状態の混合状態にあることになります。ニュートリノの場合には，同じ考えを振動現象として導くことができます。ニュートリノが生成されたときに（付随する荷電レプトンによって定義される）明確なフレーバー状態にあり，それが反応したときにも明確なフレーバー状態にあるにも関らず，その2つの反応点の間を飛んでいるときは明確なフレーバー状態にはないのです。ニュートリノが飛んでいるときの明確な固有状態はその質量であり，ニュートリノには3つの異なるタイプがあるので，質量も3つの異なる状態があります。しかし一般的には，これらの質量状態は3つの異なるフレーバー状態と完全には一致しないのです。この不一致の結果，次のようなことになります。

ニュートリノが，例えばパイ中間子の崩壊から生成されたとしましょう。それは明確なフレーバー固有状態で，この場合はミューニュートリノです。しかし，質量の固有状態ではありません。実は3種類全ての質量状態が，ある比率で混合した状態なのです。その比率は1番目の質量状態が5%，2番目の質量状態が45%，そして3番目の質量状態が50%です。
ニュートリノは生成点から飛び出して飛行していきます。すると，3つの質量状態はお互いに足並みが外れます。それらは異なる質量を持っているので，僅かに異なる速度で飛行することになります。したがって，そのニュートリノがある距離を飛んだときには，異なる質量状態の相対比率は最初にニュートリノが生成されたときとは違うものになっているでしょう。このことはそのニュートリノがもはやフレーバー固有状態にないことを意味します。なぜなら，もはや1番目，2番目，3番目の質量状態がそれぞれ5%，45%，50%ではないからです。
そのニュートリノが再び反応したときを考えます。今度はフレーバーの混合状態になっているので，ミューニュートリノとして反応する確率はいくらかありますが，電子ニュートリノやタウニュートリノとして振る舞う確率もまたいくらか持っています。もし，我々の実験がミューニュートリノを検出するセットアップしか持っていなければ，期待するよりも少ない数を検出することになるでしょう。

振動現象の数学は基本的に回転の数学と同じです。もし2つのフレーバーと2つの質量しか関与していなければ，その回転は1つの角度θで書き表すことができます。3つのフレーバーの場合には3つの角度が必要になり，その数学はもっと複雑になります。

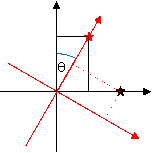
図13：回転する座標軸。黒い座標軸はフレーバー状態を表し，黒い星印は純粋な電子ニュートリノ状態にあるニュートリノを表している。角度θだけ回転した赤い座標軸は質量状態を表す。黒いニュートリノは純粋な質量状態にはないことに注意。それぞれの軸に対応する両方の質量の混合状態である。赤い星印は純粋な質量状態にあるニュートリノであるが，しかしそれはフレーバーの混合状態である。それが反応を起こしたとき，電子ニュートリノとして反応するのか，ミューニュートリノとして反応するのかは分からない。

2つのフレーバーの場合は，フレーバーαとして生成されたニュートリノがフレーバーβとして観測される確率を計算するのは非常に簡単です。それは，

P(α→β) = sin²(2θ) sin²(1.267 Δm² L/E)

のようになり，θは混合角，Δm²は(eV)²で表した質量の2乗の差 m₂² – m₁²，Lはkmで表した飛行距離，EはGeVで表したエネルギー，1.267は上記の単位で正しい結果を得るための定数です。この式において重要なことはθとΔm²はニュートリノの性質なのに対し，LとEは実験ごとに決まる量であることです。したがって，ニュートリノ実験で重要な数はL/Eという比で，もし実験のビームエネルギーが競争相手の実験の2倍であるならば，検出器を2倍遠くへ置くことで同じ測定をすることができます。（または，もしすでに検出器がある距離に置かれていれば，ニュートリノビームのエネルギーを調節することによって，最大限にビームを利用できるように設計することができます。これがT2K実験で行われたことです。）

太陽ニュートリノとMSW効果

簡単な2成分フレーバー振動は大気ニュートリノ異常をよく説明しました。しかし、太陽ニュートリノ欠損の問題はさらなる困難さを示していました。問題は以下のようです。

太陽からのニュートリノは全て同じエネルギーを持っているとは限らない。したがって，それらは全てが同じ振動数で振動するわけではない。もしL/Eが1よりもずっと大きければ，ニュートリノが太陽から地球に届く間に何度も振動を繰り返すので，確率の細かなサイン波の構造はぼやけてしまい，エネルギーに依らず1/2（2種類のニュートリノしか関与しない場合）か1/3（3種類全てのニュートリノが関与する場合）の一定値になると期待される。しかし，実際は明らかにこうなってはおらず，図10を見ると，わすかにエネルギーの異なるニュートリノが大きく異なる残存確率を持つことが分かる。
したがって，我々はきっと1回または2回だけ振動したあとのニュートリノを観測しているに違いない。そうだとすると，エネルギーEの変化が極めて小さくてもそのL/Eの違いが明確に異なる結果をもたらす。
しかし，太陽を回る地球の軌道は完全な円ではなく，6月よりも1月の方が3％ほど太陽に近づいている。もし，Eの小さな変化が振動確率に著しい変化を引き起こすのであれば，Lの小さな変化でも同じことが起こるはずである。つまり，年間を通して残存確率の変化を観測するはずであるが，実際はそうなっていない。

この問題の答えは，太陽ニュートリノが上空大気や加速器などのような真空に近いところで生成されるのではなく，太陽のコアという非常に高密度な物質の中で生成されるということにあるということが分かりました。このような高密度物質の中で，電子ニュートリノは太陽深部の高温高密度プラズマ中にある非常に多くの電子と相互作用しやすくなります。ミューオンやタウレプトンはそこには存在しないので，電子ニュートリノ以外のニュートリノは影響を受けません。この違いは振動の有効パラメーターを変化させてしまうことが明らかになり，この効果は最初にこの問題を解明した3人の理論家‐ロシア人のミケーエフ(Mikheyev)とスミルノフ(Smirnov)，アメリカ人のヴォルフェンシュタイン(Wolfenstein)‐の頭文字をとってMSW効果として知られています。

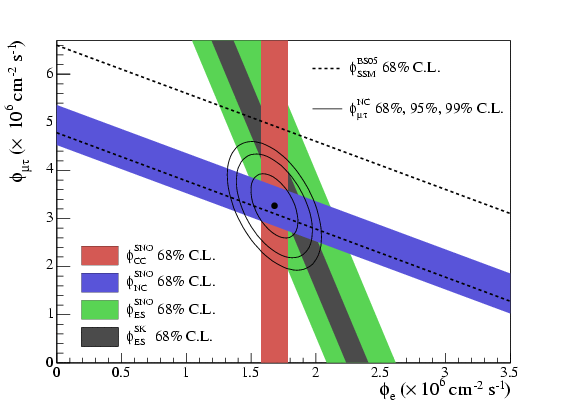
図14：SNO実験から得られたニュートリノフラックス。横軸は電子ニュートリノフラックスで縦軸は他のタイプ（μかτかの区別はできない）のニュートリノフラックスを表す。赤い帯領域は電子ニュートリノのみに感度がある荷電カレント解析の結果で，青い帯領域は全てのタイプに等しく感度がある中性カレント解析の結果である。緑の帯領域はニュートリノ－電子弾性散乱で，ほとんどが電子ニュートリノであるが他のタイプにも多少の感度がある。茶色の帯領域は同じ測定をスーパーカミオカンデで精度を上げて行ったもの。点線に挟まれた帯領域は標準太陽模型で期待される全ニュートリノフラックスである。

MSW効果の特徴は，ある状況下でそれは共鳴になり，（ほとんど）全ての電子ニュートリノが他のタイプのニュートリノに効率的に転換することです。太陽の場合，陽子・陽子連鎖反応で生成された低エネルギーニュートリノはほとんど影響を受けませんが，それより高いエネルギーのニュートリノは共鳴に達し，このことによりBe-7ニュートリノが明らかにほとんど全て欠損していることが説明できます。共鳴の特徴は，ほとんどの成分が電子ニュートリノである質量状態が，転換先の他の状態よりも（真空中で）ずっと軽い場合のみに起こるということで，したがってほとんどが電子ニュートリノで占められる質量状態は3つのうちの最も重い状態ではないということが分かります。反対に，“通常の”振動は真空中で起こり，関与する2つの状態のどちらが重いかは知ることができません。

太陽ニュートリノ欠損に関するこの説明は，重水素を使ったSNO実験によって数年後に劇的に確立されました。この実験では，ニュートリノの荷電カレント反応と中性カレント反応の比を直接比較するために，重水素の解離反応が使われました。図14に見られるように，その結果は明らかに“消失”した太陽ニュートリノは実は全く消失しておらず，単に他のタイプのニュートリノに転換したことを示しています。これはニュートリノ振動を支持する決定的な証拠です。

ニュートリノの質量

タイプαのニュートリノがタイプβのニュートリノに転換する確率は，もしΔm²=0であればゼロです。つまりニュートリノの質量がゼロであるか，または全てのニュートリノが全く同じ質量を持つ場合は，ニュートリノ振動は起こりません。これは，たとえどのようにニュートリノを分類しようとも，区別できるタイプの数は同じ，すなわち3に保たれなければならないからです。もし，3つの異なる質量がなければ，質量は有効な分類手段ではなくなります。そしてニュートリノの固有性はそれぞれの反応で定義されるしかなく，ニュートリノ振動は起こりません。このことはちょうど地図の上で場所を示すのに似ています。緯度と経度を使うこともできれば，イギリス陸地測量局の参照コードを使うこともできます。またはある基準地点からの距離と方位（例えば“鉄道の駅から5km北西に”など）を使うこともできます。しかし，いずれにしても場所の指定には2つの数量が必要です。（海面からの高さも指定したければ3つ必要になります。）

図15：太陽ニュートリノ振動に対するΔm²とθ。このプロットは太陽ニュートリノのデータとKamLANDによる原子炉ニュートリノのデータを併せたベストフィットを示している。参考文献7から引用。

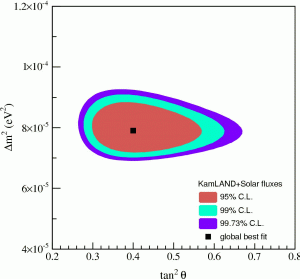
観測したニュートリノの数を数えることで，実験ではニュートリノ残存確率の式の中にある未知のΔm²とθの値を求めることができます。（式中のLとEは実験の設計値からすでに分かっています。）太陽ニュートリノと大気ニュートリノに関する最近の結果を図15，図16に示しています。明らかにパラメーターは同じではなく，予想された通りでした。太陽ニュートリノの場合は，ν_eから始まってどれか他のタイプへ転換しているのに対し，大気ニュートリノの場合はν_μから始まってν_τへ転換しています。つまり，我々は異なるシステムを見ているのです。通常，太陽ニュートリノの混合角はθ₁₂と呼ばれ，大気ニュートリノの混合角はθ₂₃と呼ばれています。

振動現象は質量の2乗差のみに感度があるため，これらの結果から質量がゼロでないことは分かりますが，それがいくらかなのかは分かりません。8×10^-5 eV²という質量1と質量2の2乗差の値は，0と0.009 eV，または0.01 eVと0.0134 eV，0.1 eVと0.1004 eV，さらには10 eVと10.000004 eVのどれにでも対応し，振動の結果はそれらのどれに当たるかは教えてくれません。大気ニュートリノの場合は，どちらの状態が重いのかさえも分かりません。2つのΔm²の値を併せると，以下の2つの可能な場合があることが分かります。

順階層: ν₁ ← 8×10^–5 → ν₂ ← 2.3×10^–3 → ν₃;

逆階層: ν₃ ← 2.3×10^–3 → ν₁ ← 8×10^–5 → ν₂.

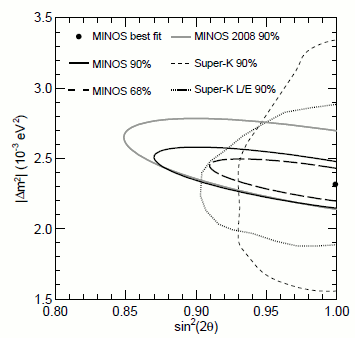
図16：大気ニュートリノ振動に対するΔm²とθ。このプロットには，スーパーカミオカンデからの大気ニュートリノのデータとMINOSからの加速器ニュートリノのデータの両方を示している。参考文献8から引用。

太陽ニュートリノのデータから質量状態1はほとんど電子ニュートリノであることが分かっています。それで，“順階層”は一番軽いニュートリノが一番軽い荷電レプトンに対応することからそう呼ばれています。図16はν_μとν_τの混合が可能な限り非常に大きい（θ23 ～ 45°）ことを示しています。したがって，質量状態2と3をそれぞれ“μ”と“τ”に割り当てるのは筋が通りません。それらはν_μとν_τをそれぞれ同量含んでいるのです。

ベータ崩壊を用いたニュートリノ質量の測定

次世代のニュートリノ振動実験は，質量状態の順序を解明できるはずです。そしてその質量差を測る精度を向上させてくれるでしょう。しかし，質量の値そのものを測定するためには，ニュートリノが存在するという発想に至った起源‐ベータ崩壊‐に立ち戻る必要があります。

ベータ崩壊では，解放されるエネルギー（放射性の親核と娘核の質量差）は電子とニュートリノの間で分配されます。しかし，電子は少なくとも自分自身の質量を作りだすに十分なエネルギーを持つ必要があるので，電子は少なくともm_ec²のエネルギーを得る必要があります。もしニュートリノの質量が厳密にゼロであれば，非常に不幸にもニュートリノのエネルギーがゼロになることもあるでしょう。しかし，ニュートリノには質量があることが分かっているので，ニュートリノは少なくともm_νc²のエネルギーを持ち去ることになります。これによって，電子に与えることのできる最大エネルギーがわずかに下がります。したがって，電子のエネルギーの分布はその高い方の終端付近でわずかに変化することになります。

残念ながら，電子とニュートリノの間で分割されるエネルギーが一方に非常に偏ることはあまりなさそうなので，どんな同位体を使っても，電子のエネルギースペクトルにおいてこの領域での崩壊数は非常に少ないと考えられます。さらに，ニュートリノの質量は極めて小さいと考えられるので，電子のエネルギーを非常に高い精度で測定する必要があります。小さな実験誤差でも簡単に信号を消し去ってしまうでしょう。電子は電荷を持っているので，そのエネルギーは電場に影響されます。エネルギーの単位であるeVは，ちょうど1Vの電位差で電子が得るエネルギーです。したがって，もし実験で電場を使うならば，その電場が測定しようとしている電子のエネルギーに影響を及ぼさないことを保証するように慎重に行わなければなりません。もし，実験で用いる同位体が化学的化合物の形態であれば，化学結合に付随している電場でさえも結果を歪めてしまうほど十分大きいかもしれません。その場合は計算によって補正を加える必要があるでしょう。要するに，これは非常に難しい実験的測定であり，原子核物理学者が長年取り組んでいるにも関らず（質量がゼロである場合の予測からの違いを検出できていないという意味で）成功に至っていないのも驚くことではありません。

ベータ崩壊から得られたニュートリノ質量の最小の上限値は，トリチウム（³HまたはTと表記）の崩壊から測られています。トリチウムはヘリウム3へ12.3年の半減期で崩壊し，以下の理由で研究に相応しい同位体です。

³Hと³Heの質量差はかなり小さく，18.6 keV（原子量0.00002）しかない。これにより，ゼロでないニュートリノ質量によって引き起こされるスペクトルの小さな歪みを観測しやすくなる。
半減期が比較的短いので，多数の崩壊を起こすためにそれほど多くのトリチウムを必要としない。
トリチウムは非常に簡単な構造の原子で，それが自然に作る分子であるT₂も非常に単純な分子である。これにより，分子の内部電場が電子のエネルギーに与える影響の計算が非常に簡単になる。

小さな質量差と短い半減期の組合せは非常に稀で，通常はもし質量差が非常に小さければ半減期は非常に長くなります。なぜなら，この場合原子は崩壊してもあまり“得をしない”からです。例えば，レニウム187という同位体は解放エネルギーの最大値がもっと低く，わずか2.6 keVですが，その半減期は430億年です。したがって，ベータ崩壊の実験が1940年代に初めて試みられて以来，実験対象の同位体としてトリチウムがほとんど毎回選ばれてきました。

これまでのところ，最もよい結果はMainzやTroitskでのトリチウムのベータ崩壊実験から得られています。両者は多少異なるトリチウム線源を使っており，Troitskでは気体トリチウムが使われ，Mainzではグラファイト基板にトリチウムを凝縮したものが使われています。しかし，実験のセットアップはお互いに非常に似ています。結果も非常に近い値が報告されており，約2 eVの上限値となっています。（言い換えれば，どちらの実験でもゼロでない質量を示す積極的な証拠は得られていないが，もし質量が2eVよりも大きい場合には何かしら観測されていたはずだったということです。）

MainzとTroitskの実験は今では新しいトリチウムベータ崩壊実験であるKATRIN実験に引き継がれており，現在建設中です。KATRINは基本的にMainzやTroitsk検出器に用いられた基本デザインをより大きくより先進的に進化させたもので，上限値の感度を10倍の0.2 eVまで向上させると期待されています。加えて，トリチウムよりも低いエネルギーであるが長寿命の同位体レニウム187を用いてMARE実験が行われています。ここでは，KATRINと同程度の感度を多少長い時間スケールで達成できると考えられています。MAREでは超低温を使った実験デザインによって¹⁸⁷Reの低い崩壊率の問題を解消しており，この実験ではレニウムは線源であると同時に検出器の役割も担っています。（次章で説明する二重ベータ崩壊実験の多くで使われているのと同じようなコンセプトです。）レニウムは純金属（しかも超伝導体：低温実験で引き出される特性）としても，化合物に組み入れた形としても両方で用いることができ，化合物の場合はAgReO₄として使います。MAREコラボレーションは両方の技術を研究し検討しています。

レニウムを用いる技術はまだトリチウム実験ほど成熟しておらず，0.2 eVの感度を達成するには多少の時間がかかると考えられますが，2つの異なった実験が非常に異なる方法を用いてこの困難な問題に挑戦することは非常に重要です。前述で見てきたように，太陽ニュートリノの欠損は2番目の実験で確かめられたときに初めて深刻に捉えられました。ニュートリノ物理学の分野は誤報の歴史であり，それが新しい結果に迫ることに対してコミュニティを保守的にしてきたのです。ゼロでない結果を報告する最初の実験が結果的には名声を得るでしょうが，それが認められるのはおそらく2番目の実験チームによる検証を待たなければならないでしょう。

マヨラナニュートリノとニュートリノレス二重ベータ崩壊

ニュートリノの標準模型的描像は，他の全てのクォークやレプトンと同じくニュートリノと反ニュートリノは明らかに異なる粒子を仮定しています。ニュートリノ以外の場合ではこのことは電荷によって確かめることができます。例えば，電子は負の電荷を持ち，その反粒子である陽電子は正の電荷を持っています。全体として電気的中性である中性子の場合であっても，それに含まれるクォークは異なる電荷（中性子は+2/3-1/3-1/3，反中性子は-2/3+1/3+1/3）を持っています。そしてこのことは散乱実験によって検証されています。力の媒介粒子とは対照的に，物質粒子ではニュートリノだけが中性であり，（我々が知る限り）真の素粒子です。このことは，ニュートリノと反ニュートリノを分ける概念に代わる別の可能性を与えます。2種類の粒子とされているものは実は同一で，スピンの向きだけが違うのでは？というものです。弱い相互作用の理論的構造のため，左巻きニュートリノはニュートリノとして反応するしかせず，一方右巻きニュートリノはあたかも反ニュートリノであるかのように反応します。右巻き左巻きの属性（ヘリシティ）が変化せず保たれる限り，その2つはたとえ原理的に同一であっても全く異なる粒子として振る舞うでしょう。

このように振る舞うニュートリノは，関連する数学的記述を最初に解明したイタリア人の理論家エットーレ・マヨラナ(Ettore Majorana)にちなんで，マヨラナニュートリノと呼ばれます。もしニュートリノが正確に質量ゼロであれば，そのヘリシティは固定され，2つの描像の違いは意味が無くなります。全てのニュートリノは常に左巻きで，全ての反ニュートリノは右巻きになります。しかし，振動現象はニュートリノが正確には質量ゼロではないことを教えてくれました。そして，質量ゼロでなければ，それらのヘリシティは変化しない定数ではなくなります。したがって，もしニュートリノが本当にマヨラナ粒子であれば，ニュートリノとして生成された粒子が引き続いて反ニュートリノとして相互作用することが原理的に可能になります。（実際には非常に起こりにくいとすれば，それは質量が非常に小さいからということができます。）この現象は二重ベータ崩壊という非常に稀な放射性崩壊に見られる可能性があります。

通常，ベータ崩壊は原子が中性子を陽子に変換（電子を放出し原子番号は1つ増加）する場合や，陽子を中性子に変換（陽電子を放出し原子番号は1つ減少）するときに起こります。これは隣の同重体（同じ原子番号，すなわち同じ総数の陽子と中性子を持つ原子核を同重体と呼ぶ。）がベータ崩壊する原子核よりも強く結合し，したがってそれがより軽い場合に起こります。しかし，ある状況下では，隣の同重体が問題にしている原子よりも重い場合でも，原子番号が2つ離れた同重体の1つがそれよりも軽い場合があります。この場合，ただ1つ許される崩壊モードが二重ベータ崩壊です。そこでは原子核は同時に2個の電子を放出します。（そして標準模型では2つのニュートリノも同時に放出され，この過程は2νββ崩壊として知られています。）これは非常に起こりにくい事象で，したがってそのような同重体の寿命は宇宙の年齢よりもずっと長く（少なくとも10¹⁹年に）なります。ほとんどの場合，二重ベータ崩壊でしか崩壊しない同位体は安定と見なすことができます。実際，60種程度の原理的にこのように崩壊できる核種のうち，11種しか二重ベータ崩壊することが観測されていません。

2νββ崩壊はもともとの標準模型に現れる質量ゼロのニュートリノと完全に無矛盾です。しかし，もしニュートリノがマヨラナ粒子であれば，この崩壊の別の型が可能になり，そこではベータ崩壊の1つでニュートリノとして放出された粒子が，別のベータ崩壊で反ニュートリノとして吸収され，図17に示したようなニュートリノレス二重ベータ崩壊（0νββ）になります。

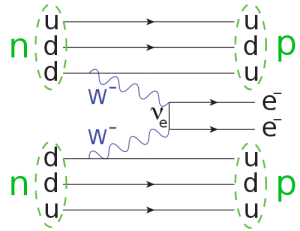
図17：二重ベータ崩壊。2個の中性子が2個の電子の放出とともに2個の陽子に転換する。崩壊のうちの1つから放出されたニュートリノがもう1つの崩壊によって反ニュートリノとして吸収される。図はWikimedia Commonsから引用。

二重ベータ崩壊はレプトン数保存則を2つ破っています。2個の電子が対応する反レプトン無しに生成されるからです。それはニュートリノがマヨラナ粒子であるときだけ可能です。したがってそれが発見されれば，質量の値だけでなくニュートリノの本質を確立することになるでしょう。（ここでは電子を生成するので，ダイアグラムの中のニュートリノは電子ニュートリノです。したがって質量の固有状態ではなく，測定される質量は3つの可能な値の荷重平均になります。）

0νββ崩壊の信号は互いに反対方向に生成される2個の電子で，それぞれが（親核と娘核の質量差の半分に対応する）同じエネルギーを持ちます。対照的に，2νββでは電子は図1（の赤いライン）と同じように連続したエネルギースペクトルで放出されます。全ての0νββ同位体はもちろん2νββでも崩壊します。したがって，実験を成功に導く鍵はスペクトルの終端に小さなピークを検出することができるかどうかです。そしてそれは，少なくとも10²⁵年という2νββ崩壊よりも100万倍も長い0νββ崩壊の寿命に対応するまさに小さなピークなのです。

0νββ実験において鍵となる重要な条件はバックグラウンドを最小化することです。なぜなら，信号が非常に小さいので，期待されるピーク位置の近くでは少量のバックグラウンドでさえも実験感度に深刻な影響を与えてしまうからです。潜在的なバックグラウンドには以下のものが含まれます。

（不純物が原因の）線源自体や検出器，またはその周りの環境に含まれる自然放射能－これを最小化するには実験自体において超純粋物質を使用し，環境から上手く遮蔽することが要求されます。
宇宙線や宇宙線との相互作用で生じた放射能－これにより実験装置は通常地下に置かれ，さらには地下で製作されるのが理想的です。
2νββモード－これは避けることができません。しかし，電子のエネルギーやそれらが互いに反対方向に放出されるトポロジーによって0νββ信号と区別可能です。

二重ベータ崩壊実験において用いられる基本的な実験テクニックには次の2つがあります。1つは線源=検出器（測定される同位体が崩壊を測定するために使われる検出器自体もしくは検出器の一部）というもので，もう1つは検出能力を持たない受動的線源（同位体は検出器の一部ではない）というものです。前者のタイプは通常崩壊電子によって生成されたイオン化を測定するための冷却された固体検出器です。それらの検出器は高いエネルギー分解能を持ち，それはバックグラウンドを削減するために重要な要素です。そして非常に小さく，このことは周りの放射能から遮蔽することを容易にします。ほとんどの実験ではさらにバックグラウンドから信号を区別するために信号パルスの形を利用します。例えば，宇宙線との相互作用で生じた中性子は電子とは異なる形になります。

検出能力を持たない受動的線源の場合は，同位体は薄膜の形で検出器に囲まれる形で置かれます。これらの実験は普通それほど高いエネルギー分解能は持ちませんが，飛跡検出能力（線源＝検出器の実験では一般的にありません。）を持つので，バックグラウンドを少なくするために互いに反対方向に2個の電子が放出されるトポロジーを使うことができます。それらには同じ検出器で（ときには同時に）多くの種類の同位体を研究することができるという利点があります。

二重ベータ崩壊同位体である¹³⁶Xeは固体ではなく希ガスであるために特別なケースです。¹³⁶Xeは受動的線源の実験で使われるものと同じように，気体または液体の形で飛跡検出器の媒体として使うことができます。また物質量数トン級の暗黒物質探索実験でよく使われる候補で，そのうちのいくつかは原理的に二重ベータ崩壊実験を兼ねています。残念ながら，二重ベータ崩壊同位体は天然のキセノンのうち比較的存在比率が小さく（8.86%），性能を最適化するためにはキセノンを非常に高く濃縮する必要があります。

ほとんどの二重ベータ崩壊実験は2νββ崩壊を測定し0νββ崩壊の上限値を設定してきました。ハイデルベルグ－モスクワの実験チームが⁷⁶Geの0νββを検出したという議論を呼んでいる発表があります。質量にして0.4 eV（核行列要素を使った核物理計算の理論的誤差からくる2倍の不定性を含む）に対応しています。この結果ではスペクトルの終端領域にいくつかのピークがあるために大きな異議が唱えられ，終端エネルギーに一致しているピークもそれらの1つに過ぎないのではないかという批判を説得することができていません。GERDA実験は同じ同位体をより多くの量と高い感度で用いて，この議論を呼んでいる発表を検証もしくは反証するために設計されています。現在はコミッショニング中です。

いくつかのニュートリノレス二重ベータ崩壊実験が現在稼働中，コミッショニング中または建設中で，その全てが0.1 eVかさらに良い感度で計画されています。（Wikipedia article を参照）実験は広い範囲の同位体をカバーしていますが，崩壊率を予言したりニュートリノ質量を推測する観点から何かしらの信号を解釈したりするために必要な核行列要素の理論計算は大きな誤差を持っており，異なる核種からの信号を比較することはこの誤差を小さくする大きな助けになるでしょう。この感度を達成するのは，ニュートリノレス二重ベータ崩壊の方が単体のベータ崩壊よりも容易に見えますが，トリチウムやレニウムのベータ崩壊実験はどのタイプのニュートリノにも適用できるのに対し，二重ベータ崩壊実験はマヨラナニュートリノでないといけないことを思い起こすことが必要です。

宇宙物理や宇宙論からのニュートリノ質量

ニュートリノは宇宙において極めて当たり前の存在です。星は膨大な数のニュートリノを生成し，ビッグバンの最初の数秒間にはそれよりもずっと大量のニュートリノを作りだしました。かつて，ニュートリノが10 eVくらいの質量を持てば暗黒物質を説明できると考えられたときがありましたが，宇宙の構造を形成するシミュレーションを行ったところ，そのような速く運動する粒子は間違った形の大規模構造を作ってしまうことが分かりました。そこでは，超銀河団のような非常に大きなオブジェクトが最初にでき，銀河のような小さなオブジェクトはそのかなり後で作られます。（トップダウン構造生成）　しかし，我々が見ている宇宙は銀河サイズの構造が最初に作られ，その後それらが集まってより大きな系を作ったという歴史（ボトムアップ構造生成）の方により一致しています。このことは極めて遅く運動し，おそらくもっと重い暗黒物質粒子を示唆しています。

しかし，ニュートリノは非常に多く存在する（計算によれば宇宙のあらゆるところで1cm³に平均336個）ので，我々が現在考えているような0.1 eVのオーダーの質量を持つずっと軽いニュートリノでも，宇宙の密度にいくらか寄与していると考えられます。これはWMAP衛星（もうすぐPlanck衛星でも）によって測定された宇宙マイクロ波背景放射における温度変化のスペクトルへの影響を通して検出することができます。7年にわたるWMAPデータサンプル[9]の解析の結果，∑m_ν < 0.58 eVという上限値が見積もられました。これは宇宙背景放射，銀河の赤方偏移測定，およびハッブル定数の精密測定を併せた解析によって得られたものです。額面通りに受け取ると，これは現在得られている中でニュートリノ質量に対するもっとも厳しい制限ですが，しかしここには前提としている宇宙論モデルに関していくつかの仮定（特に宇宙は平坦で，暗黒エネルギーは宇宙定数で記述されるという仮定）をしています。これらは正しいことが保証されているわけではなく，したがって見積もられた上限値もまだ絶対ということではありません。

超新星1987Aもまたニュートリノ質量の上限値を設定するのに使われました。もしニュートリノが質量ゼロであれば，全てのニュートリノは光速で飛行します。しかし，ニュートリノは正確に質量ゼロではないので，光速より遅く飛行し，その速度はエネルギーに依存します。（よりエネルギーの高いニュートリノはより速く飛行します。）　したがって，SN1987Aから到来するエネルギーのより高いニュートリノがエネルギーの低いニュートリノよりも早く届けば，到来するニュートリノの時間分布からその質量を推察することができます。

この方法は超新星からのニュートリノパルスが瞬間的なものであれば非常にうまくいくでしょう。しかし残念ながら図7に示されたようにそうではなく，ニュートリノ放出のもともとの時間分布を考慮に入れる必要があります。さらに，ニュートリノの平均エネルギーも爆発が進むにつれて変化します。多くのニュートリノサンプルがあればこれらの効果を解決することもできるでしょうが，SN1987Aからの20個程度（カミオカンデIIとIMB検出器の時刻が同期されていなかったので，これらのうち全てが問題なく比較できるわけではない）のニュートリノでは，それはあまりできそうもなく，得られた上限値も競合できるほどよくありませんでした。

標準模型を超えて