The principles of neutrino sources and neutrino experiments have changed remarkably little since the pioneering days of the late 1950s. In a 1960 review article[3], Fred Reines made the following points:
- fission reactors are the best source of low energy antineutrinos;
- muon-neutrinos and antineutrinos can be produced by allowing pions of the appropriate charge to decay in flight, and then stopping the non-neutrino products with a dense absorber;
- such neutrino beams could be used to test whether muon-neutrinos are distinct from electron-neutrinos;
- elastic neutrino-electron scattering is a clean way to detect low-energy neutrinos if the background can be controlled;
- the reaction ν + Cl37 → Ar37 + e– could be used to detect solar neutrinos;
- detection of Cherenkov radiation from charged leptons produced by neutrino interactions in water is a promising technique, and might provide directional information;
- the Sun is a “most copious source of neutrinos”, but the neutrinos from the dominant process are of very low energy, so the detectability of solar neutrinos relies on the presence of fusion side chains giving higher-energy neutrinos from boron-8 and beryllium-7;
- cosmic rays striking the Earth’s atmosphere should produce a significant flux of neutrinos from pion decay;
- high-energy neutrinos produced by astrophysical objects would provide information not available from cosmic rays (because they are deflected by the Galaxy’s magnetic field) or photons (because they are absorbed by dense matter);
- such neutrinos could be studied by using large detectors located deep underground.
As a sketch of the next 50 years of neutrino physics, this has an impressive hit rate: only the study of neutrino masses by means of single and double beta decay is omitted. It is true that Reines thought that some aspects of this programme, such as the need for kiloton scale detectors, were impractical – nevertheless, it shows that the questions and challenges posed by the neutrino sector were recognised from the very beginning of the field. The results of addressing those challenges, however, have not been so predictable.
In this page we discuss neutrino sources, both artificial and natural. The next page considers the various methods by which these neutrinos are detected by experiments.
Artificial neutrino sources
To date, artificial neutrino sources have remained very similar to those used by the pioneers. The two principal types are fission reactors, producing electron-type antineutrinos from beta decays of fission fragments, and proton accelerators, producing muon neutrinos (or antineutrinos) from pion decays in flight.
Reactor neutrinos
Fission reactors generate energy by breaking heavy nuclei (usually U-235) into smaller fragments. As the ratio of neutrons to protons in atomic nuclei increases as the atomic mass increases, these fission fragments have too many neutrons, and are unstable, decaying by a cascade of beta decays into stable nuclei with a lower ratio of neutrons to protons. On average, each fission yields about 200 MeV of energy and about 6 electron-type antineutrinos. It is therefore possible to estimate the number of neutrinos produced per second from the power output of the reactor.
Unfortunately, neutrino experiments need to know not just the total number of neutrinos, but also their energy distribution: the probability that a neutrino will interact in your detector depends on its energy, and the physics being studied, such as neutrino oscillations, is also energy-dependent. Calculating this is a much more difficult problem, because the original uranium nucleus can fragment in different ways producing a variety of different unstable isotopes, and additional fissionable isotopes such as plutomium-239 (produced when a neutron is captured by a nucleus of uranium-238), Pu-241 (produced when a U-238 nucleus captures several neutrons before beta-decaying to plutonium) and U-238 itself (not normally fissionable, but fission can be induced if the nucleus is struck by a fast neutron) must also be taken into account. Two techniques are employed to determine the resultant energy spectrum:
- The spectrum can be calculated from first principles, using data gathered over the past 60 years on fission products and their beta-decay spectra. This is a huge calculation, requiring information on literally thousands of different beta decays, but is possible with modern computational techniques.
- Beta decays produce electrons as well as neutrinos, and the energy spectrum of the electrons can be measured directly. The neutrino spectrum can then be inferred from the electron spectrum; some information on the underlying beta decays is still required, but not as much as for the first-principles calculation. Detailed measurements of the electron spectrum from a nuclear reactor were made in the 1980s using the research reactor at the Institut Laue-Langevin in Grenoble.
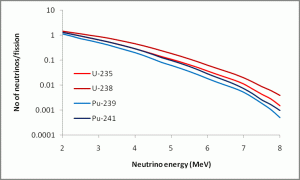
Figure 2: calculated antineutrino spectra for the four main isotopes involved in nuclear reactor power generation. The spectra are normalised to one fission: in fact U-235 and Pu-239 are the dominant isotopes, with U-238 and Pu-241 together contributing about 10% of the total. Data from T.A. Mueller et al., arXiv hep-ex/1101.2663v3.
The results of a recent calculation are shown in figure 2. The proportion of the total power that comes from U-235 and Pu-239 varies through the reactor fuel cycle, because Pu-239 is not present in the original fuel rods but is produced in the reactor itself. The spectra are all fairly similar, producing antineutrinos with energies of a few MeV. The fact that this energy is much less than the rest mass of the muon (mμc2 = 105.7 MeV) restricts the types of experiments that can be done with reactor neutrinos.
Even with all the effort that has gone into making these calculations, our understanding of these spectra remains an important contributor to the experimental error budget of experiments using reactor neutrinos. For this reason, modern reactor neutrino experiments use two detectors, a near detector close to the reactor and a far detector at a carefully selected distance (see the section on neutrino oscillations): ratios between near and far detectors can be used to study how the properties of the beam evolve with distance, and the uncertainty in the reactor neutrino flux largely cancels out.
Accelerator neutrinos
Neutrino beams from proton accelerators are produced as follows:
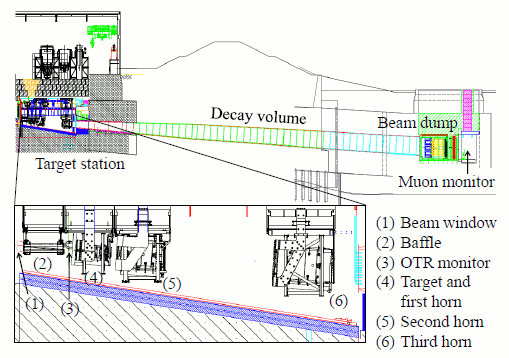
Figure 3: the T2K neutrino beamline from the target station to the beam dump. The components of the beamline are labelled in the figure; “OTR monitor” stands for “optical transition radiation”, and is used to monitor the proton beam profile immediately before it hits the target. The first horn, which surrounds the target, is used to collect positive pions; the second and third horns focus them into a collimated beam. The baffle protects the first horn from any accidental misalignment of the proton beam.
- Protons are accelerated in a standard particle accelerator (normally a synchrotron). The energy of the protons, along with the geometry of the beamline, determines the energy of the neutrinos.
- A proton beam is extracted from the accelerator and directed on to a target. The protons interact with the target material, producing a large number of secondary pions (among other particles).
- Shaped magnetic fields (focusing horns) are used to select out pions of the preferred charge (positive for a neutrino beam, negative for an antineutrino beam) and focus them into a collimated beam.
- The beam is directed into a long decay volume, where the pions decay into muons and (anti)neutrinos. Charged pions have an average lifetime of 0.026 μs (26 billionths of a second), whereas muons live for nearly 100 times as long (2.2 μs): the length of the decay volume is designed so that most of the pions decay, but very few muons do. (Note that it is necessary to take relativistic time dilation into account when calculating this: the pions are travelling at close to the speed of light, and their internal clocks will tick much more slowly than that of a stationary observer, so they will appear to live much longer than 0.026 μs. The T2K decay volume is 96 m long, not 7.8 m as one might naïvely expect.)
- At the end of the decay volume is a beam dump: a large mass of material which absorbs all the particles except the neutrinos (and a few of the muons, which are used to monitor the position and intensity of the beam).
This procedure results in a nearly pure beam of muon-neutrinos (or muon-antineutrinos if negatively charged pions are selected). The neutrino energy spectrum can be calculated from the beam parameters – this is a rather simpler task than calculating the reactor spectrum – and/or derived from the measured muon spectrum. There is some inevitable contamination with electron-neutrinos, mostly because the original pion beam also includes some kaons, which can decay to produce electron-neutrinos. Therefore, accelerator-based neutrino experiments, like reactor experiments, generally use a near detector as well as a far detector.
The energy spectrum of the neutrino beam generated in this way is rather broad: figure 4 shows the beam used by the MINOS detector at Fermilab. This can be greatly improved if the beam is deliberately offset slightly from the direction of the far detector: such an off-axis beam has a much smaller energy spread, at the cost of reduced intensity. If the proton beam is powerful enough, this is a worthwhile trade-off, and the T2K experiment uses an off-axis beam to generate a neutrino beam of comparatively well-defined energy.
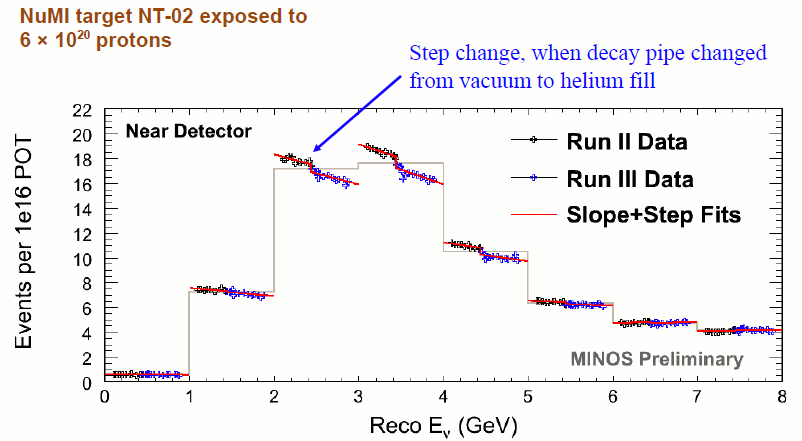
Figure 4: the reconstructed neutrino energy spectrum for the MINOS beam, showing the slight decrease in intensity with time, which is believed to arise from the aging of the target. Picture taken from the MINOS public plots webpage.
Future techniques
Although the specifications of the accelerators have improved dramatically, the above method of producing a neutrino beam from an accelerator is conceptually identical to that described by Fred Reines in his 1960 review and constructed by Lederman, Schwartz and Steinberger in their Nobel-winning 1962 experiment. All currently available neutrino beams are generated in this way, but genuinely new techniques are on the horizon for the next generation.
Beta decays generate very pure samples of electron antineutrinos (if an electron is emitted) or neutrinos (if a positron is emitted), but the energies of the neutrinos are too low for many experimental techniques: in particular, because E < mμc2, the neutrinos cannot convert to muons (and still less to the much heavier taus). The idea of the beta beam is to increase the neutrino energy by stripping the electrons off the radioactive isotope and then accelerating the positively charged ion to high energies before it decays. This boosts the energy of the neutrinos produced, and also collimates them into a fairly narrow beam. If the chosen isotope decays by electron capture (instead of emitting a positron and a neutrino, it captures one of its own orbital electrons and just emits a neutrino, e– + p → νe + n), the beam also has a very well-defined energy, although such beams are harder to make because you have to ensure that the nucleus manages to keep hold of one electron while it is being accelerated (it can’t decay by electron capture if there isn’t an electron to capture!).
Beta-beams have to use short-lived artificial isotopes, since a long-lived isotope such as carbon-14 would not produce enough neutrinos. Although acceleration of ions is a well-established technique (for example, the LHC has been used to collide lead nuclei), these very short-lived ions present special problems: they must be collected and accelerated quickly, before too many of them decay, and when they do decay they are lost from the beam (because their electric charge changes) and may cause the material of the accelerator to become radioactive. Radiation safety, both for the machine and for the personnel, becomes an important issue.
Although nobody has built a beta-beam so far, the technique is being intensively studied, especially at CERN, which has considerable expertise in the acceleration and storage of ions.
The ultimate accelerator-derived neutrino beam is the Neutrino Factory, which generates neutrinos by the decay of muons stored in a particle accelerator. The muons decay by μ+ → e+ νe νμ: this is an extremely simple and well-understood decay and the neutrino spectra can be calculated with great precision. Although the beam is mixed, the antineutrinos are all muon-type and the neutrinos are all electron-type (swap these round if μ– are used), so they are easy to distinguish provided that your detector can determine the charge of the produced electron or muon (antineutrinos always convert to positively charged leptons and vice versa).
This is a powerful and elegant technique. The problem is that muons live for only 2.2 microseconds on average: although this is greatly extended by relativistic time dilation, even muons accelerated to 50 GeV only live for a millisecond. This means that the muons must be made, “cooled” (have their random motions reduced so that they form a nice collimated beam), accelerated and stored within a very small fraction of a second, which is a very challenging technical problem. Theoretical studies show that neutrino factories have the greatest potential for increasing our understanding of neutrinos, so this technical challenge is being addressed: for example, the Muon Ionisation Cooling Experiment (MICE) is a feasibility study aimed at showing that muons produced from pion decay can indeed be cooled into a beam suitable for acceleration and storage. However, this is still at quite an early stage, and an operational Neutrino Factory must be at least a decade away.
Astrophysical neutrino sources
One of the most important discoveries in neutrino physics, the phenomenon of neutrino oscillations, came about not through the use of artificial neutrino sources, but by using neutrinos produced naturally in the Sun and in the Earth’s atmosphere. Astrophysical neutrinos can provide information both on the physics of neutrinos and on important astrophysical phenomena such as supernovae and active galaxies.
Solar neutrinos
The Sun generates energy by fusing hydrogen to helium, as first suggested by Sir Arthur Eddington as long ago as 1920. Since hydrogen contains only protons while helium has two protons and two neutrons, this process must inevitably involve the conversion of protons to neutrons, and therefore the emission of neutrinos. The process by which this is done, the pp chain, was worked out by Hans Bethe in the late 1930s, and is shown in Figure 5[4].
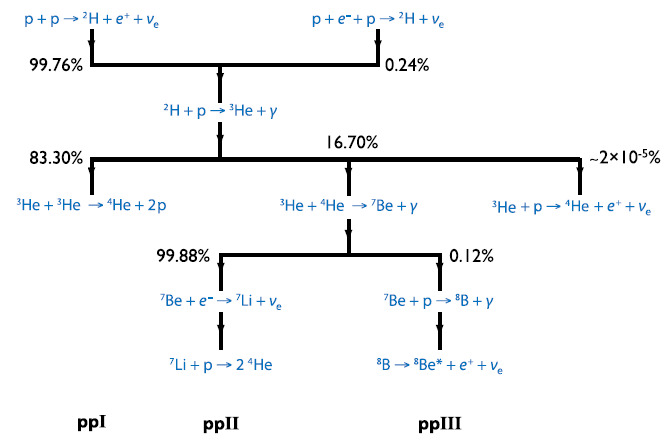
Figure 5: the pp chain, showing the principal branches and branching fractions. The neutrinos emitted in this series of reactions are known as pp (from the reaction at top left), Be-7 (in pp II branch), B-8 (pp III), pep (top right) and hep (centre right). Figure from reference 4.
The neutrino flux from the Sun is enormous: about 60 billion per square centimetre per second. Even given the neutrino’s reluctance to interact, it seems that detecting solar neutrinos should be a reasonably practical task. Unfortunately, the vast majority of solar neutrinos come from the initial deuterium production, p + p → 2H + e+ + ν (pp neutrinos), and these have very low energy, < 0.42 MeV. Most methods of neutrino detection are not sensitive to such low-energy neutrinos, so most experiments rely on the higher energy Be-7 and B-8 neutrinos produced in the pp-II and pp-III side chains (the pep and hep neutrinos (see figure 5) also have high energies, but are very rare).
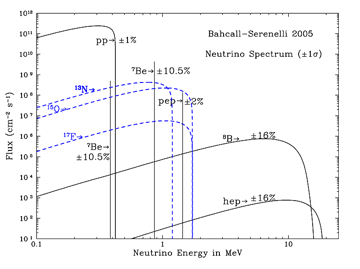
Figure 6: energy spectrum of solar neutrinos. Most solar neutrino detectors are dominated by the Be-7 neutrinos and the B-8 neutrinos, because of their higher energies. The blue dotted lines are neutrino spectra from the CNO cycle, which contributes about 1% of the Sun’s energy generation. Figure from John Bahcall.
Solar neutrinos were first detected by Ray Davis, using the chlorine capture reaction ν + 37Cl → 37Ar + e–. This reaction is only sensitive to electron-neutrinos with energies above 0.814 MeV, so it detects primarily neutrinos from Be-7 and B-8 (see figure 6). Famously, the experiment detected only about 1/3 of the predicted number of neutrinos, thus initiating the Solar Neutrino Problem. At first, it was not clear if this was a “solar problem” (perhaps the theoretical models of the Sun’s structure were not quite right), a “neutrino problem” (the theoretical model of the neutrino was not right), or an experimental problem (Davis’ calculation of his efficiency in detecting Ar-37 was not right). It took many years, and many more experiments, before the second interpretation was confirmed as the correct one.
Solar neutrinos have been instrumental in studying neutrino oscillations; results from solar neutrino experiments are still a key input into calculations of neutrino mixing angles.
Supernova neutrinos
Supernovae mark the explosive deaths of stars. For a brief period, the exploding star becomes comparable in brightness to its entire host galaxy; the Galactic supernova seen in 1006 was much brighter than Venus, and was visible in daylight for weeks, despite being over 7000 light-years away. Unfortunately for astronomers, no supernovae have been seen in our Galaxy since Kepler’s Supernova in 1604, but SN 1987A, a supernova observed in the Large Magellanic Cloud – a small satellite galaxy of the Milky Way, about 160000 light years away – has the distinction of being the only astrophysical object other than the Sun definitively detected as a neutrino source.
There are two main types of supernovae. Type Ia supernovae, which are extensively used by cosmologists because they all have very similar intrinsic brightness, are believed to originate in the explosive destruction of a white dwarf star which has become too massive to support itself against gravity. SNe Ia are the brightest type of supernova (SN 1006 was probably a type Ia), but are not expected to produce many neutrinos.
Core-collapse supernovae (variously designated Ib, Ic, IIb, II-P and II-N depending on details of their spectra and light-curves) arise when a massive star comes to the end of its life. All stars generate energy from nuclear fusion reactions, initially using hydrogen; when the hydrogen in the central regions runs out, stars like the Sun will eventually switch to fusing helium into carbon – which requires much higher central temperatures, about 100 million kelvin as opposed to 10 million for hydrogen fusion – before dying as a white dwarf. Stars with more than 8 times the mass of the Sun can continue this process of fusing heavier elements through successively heavier isotopes, until they form a core of iron.
Iron is the most stable element: the binding energy of its nucleus is greater than the elements on either side. Elements lighter than iron can release energy by fusion; elements heavier than iron can release energy by fission; but nothing that you do to iron can release energy. As a result, once the star has formed an iron core, it is doomed. When the core becomes too massive to support itself against gravity, it collapses, and in these conditions of extreme heat and pressure the protons and electrons combine together to form neutrons, releasing electron-neutrinos. Conditions are so hot that even more neutrinos are made thermally, as neutrino-antineutrino pairs: in fact, even though to us it’s the light from the supernova that is spectacular, 99% of the energy released by a core-collapse supernova comes in the form of neutrinos[5].
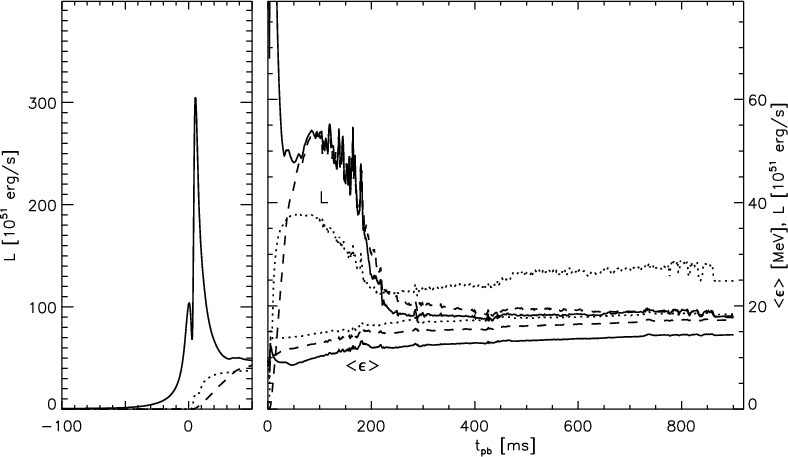
Figure 7: simulation of neutrino spectra from a core-collapse supernova produced by a 15 solar mass star. Solid line, νe; dashed line, anti-νe; dotted line, all other species. In the right-hand plot, the upper lines are the luminosity and the lower lines are the mean energy. The sharp peak at t = 0 is the neutronisation pulse, when the protons in the core are converted to neutrons; the rest of the neutrinos are produced thermally. This spectrum is calculated for an observer 400 km from the collapsing core. Figure from reference 5.
Neutrinos are crucial to the understanding of core-collapse supernovae. Simulations suggest that without the neutrino contribution, the star would not explode: a shock-wave is generated when the collapsing stellar envelope hits the newly formed neutron star, but it stalls in the dense medium, and is only restarted by the neutrinos. The “neutrino-driven winds” in core-collapse supernovae are also a favoured site for the so-called r-process of heavy-element building, responsible for about half the abundance of elements heavier than iron. Thus, neutrino production in core-collapse supernovae is an essential ingredient in understanding the chemical evolution of the Galaxy. Furthermore, the neutrinos come from much deeper in the stellar collapse than the light, and therefore have the potential to provide information from much closer to the initial neutron star formation.
The neutrinos from Supernova 1987A
SN 1987A was discovered just after midnight (UT) on February 24, 1987, by Ian Shelton; it was the first naked-eye supernova for nearly 400 years. Subsequent examination of earlier photographs showed that the supernova had been visible about 14 hours earlier (it was then at magnitude 6, compared to magnitude 12 for the pre-supernova star). It represented the explosion of a previously catalogued star called Sanduleak –69° 202, a blue supergiant about 20 times as massive as the Sun. This was the first time that good information, including spectra, had been available for the progenitor star of a supernova: all other modern supernovae had been observed in more distant galaxies where information on individual stars is not usually available.
The neutrino burst associated with SN 1987A was observed at 07:35:41 UT on February 23, about 3 hours before the first observation that the star had brightened in visible light (and about 5 hours after the last observation in which it definitely had not brightened). Eight neutrinos were seen by the Irvine-Michigan-Brookhaven (IMB) experiment, and 11 by the Kamiokande-II experiment (both were water Cherenkov detectors). A further 5 events were observed at the liquid scintillator Baksan detector at a time consistent with these, but this signal is much less statistically significant. An apparently significant burst observed about 4½ hours earlier by the Mont Blanc liquid scintillator detector did not correspond to a signal in any of the other detectors, and is generally assumed to have been an unlikely accidental coincidence: it is very difficult to understand two neutrino bursts 5 hours apart from the same core collapse, and nothing was seen in the larger K-II detector. (IMB had a much higher energy threshold and probably would not have seen these events.)
The neutrinos from SN 1987A generated an enormous amount of theoretical interest. From the known neutrino interaction rate and the energies of the detected neutrinos, it was possible to work out (within about a factor of 2) the amount of energy that SN 1987A must have released in neutrinos: the answer is about 3×1046 J, corresponding (using E = mc2) to a mass of 3×1029 kg. This is about 1/6 of the mass of the Sun, and confirms that most of the energy released by a core-collapse supernova is in the form of neutrinos. It is consistent with the calculated binding energy of a neutron star.
In principle, the time and energy distribution of neutrinos from a supernova could tell us a great deal about the supernova explosion, and perhaps quite a lot about neutrino physics too. The numbers detected from SN 1987A were simply too small to do very much – not that this is reflected in the huge number of theoretical papers published on the subject! – but a supernova in our Galaxy, perhaps five times closer, would produce thousands of detected neutrinos in today’s larger detectors (Super-Kamiokande is 25 times the size of Kamiokande-II). We can only wait and hope!
Atmospheric neutrinos
The Earth is constantly bombarded by cosmic-ray particles from space. Outside the Earth’s atmosphere, these are mainly protons, with around 10–15% heavier nuclei, consistent with the general chemical composition of interstellar matter. When they hit the atmosphere, these high-energy protons interact with air molecules to produce showers of pions, which subsequently decay to muons and muon-neutrinos; some of the muons reach the ground and are detected as cosmic rays, while others decay in flight to produce more muon-neutrinos and electron-neutrinos as well. This process is exactly similar to that used to produce neutrino beams from particle accelerators. If all the muons decayed before reaching the ground, we would expect to see two muon-neutrinos for every electron-neutrino (one muon-neutrino associated with the production of the muon, one of each produced when it decays): they don’t all decay, so the actual expected ratio is somewhat more than this. Early observations of atmospheric neutrinos were contradictory, with some experiments observing approximately the expected ratio while others saw significantly fewer muon-neutrinos than expected: the Atmospheric Neutrino Anomaly. After some years of disagreement, data from Super-Kamiokande finally convinced everyone that the deficit was real and a consequence of neutrino oscillations. This is generally regarded as the first definitive evidence for neutrino oscillation, although the solar neutrino experiments have some cause to feel hard done by in this.
Atmospheric neutrinos are produced with a very wide range of energies, because the primary cosmic-ray particles also have a huge energy range. Depending on your point of view, they are either an invaluable laboratory to study neutrino oscillations, or an irritating background to searches for high-energy neutrinos from astrophysical sources. Certainly, Fred Reines’ 1960 opinion that atmospheric neutrinos would not be of much intrinsic interest has turned out to be unduly pessimistic!
Neutrinos from astrophysical accelerators
Atmospheric neutrinos are created by interactions of cosmic rays with our atmosphere – but where do the cosmic rays themselves come from? This question is not easy to answer, because cosmic rays are charged particles and therefore are deflected by the Galaxy’s magnetic field as they travel through space. By the time they hit the Earth’s atmosphere, their directions no longer give any information about their point of origin. Plausible theories suggest that most cosmic rays may come from supernova remnants – the expanding gas clouds left after a stellar explosion – while the most energetic examples may originate in active galaxies or gamma-ray bursts, but there is no proof of any of these hypotheses.
Whatever they are, the sources of cosmic rays are clearly accelerating protons to very high energies. It is inevitable that some of these high energy protons will collide with other particles, or with photons, within the source, generating pions and hence producing neutrinos. Therefore, every source of high-energy protons should also be a source of somewhat less high-energy neutrinos (the neutrinos carry only a fraction of the energy of the protons that produced them). These neutrinos will not be affected by the Galaxy’s magnetic field, so observing them will provide clear evidence of the sites of astrophysical particle accelerators.
This is a difficult task. The number of neutrinos is small compared to the fluxes from reactors, accelerators, the Sun or Galactic supernovae, so the detectors need to be extremely large to compensate for this. In addition, the identification of muons produced by cosmic muon-neutrinos is complicated by the large background of cosmic-ray muons, and the smaller but more intractable background from atmospheric muon-neutrinos. The first background can be alleviated by looking for muons coming upwards through the Earth instead of downwards from the sky – the neutrinos will go through the Earth without difficulty, but the cosmic-ray muons will be stopped. The second is unavoidable (atmospheric neutrinos are genuine neutrinos): you just have to measure it and subtract it from any signal.
The need for very large detectors is satisfied by using natural water as a Cherenkov radiator, instead of water in tanks. The three currently operating neutrino telescopes, IceCube, ANTARES and Baikal, use Antarctic ice, the Mediterranean Sea, and Lake Baikal respectively: they are all at least 1 km underwater (or ice) to reduce cosmic-ray backgrounds. For neutrino energies less than ~106 GeV, cosmic backgrounds are reduced still further by concentrating on upward-going events: neutrinos can pass through the mass of the Earth while cosmic-ray muons cannot. However, this does not work for the highest energies, at which the astrophysical signal is most easily detected: the interaction cross-section for neutrinos increases with energy, and for ultra-high-energy neutrinos the Earth is not transparent. IceCube, the largest of the neutrino telescopes and the only one to have detected a signal so far, can veto cosmic-ray events by using a surface array of cosmic-ray detectors – this technique is not available to ANTARES and Baikal, which are located in liquid water rather than ice.
Although IceCube has detected a flux of extraterrestrial high-energy neutrinos, so far it has identified only one point source. A high-energy muon neutrino detected in 2017 (IceCube-170922A) was found to have probably come from the blazar TXS 0506+056. A blazar is a type of active galactic nucleus, and this particular blazar was also undergoing a gamma-ray flare when the neutrino was detected, which is possibly significant as gamma rays can originate from π0 decays in the same way that neutrinos originate from the decays of charged pions. A search of archival IceCube data found evidence for an earlier detection of neutrinos from this source in 2014/15, so overall the evidence for TXS 0506+056 being a source of high-energy neutrinos, and therefore an accelerator of high-energy hadrons, is strong. However, IceCube has also presented data showing that most of its observed astrophysical neutrino flux does not originate from blazars, so the origin of high-energy cosmic rays remains an unsolved puzzle.
Neutrinos from dark matter
The nature of dark matter is one of the most intriguing unsolved mysteries of modern cosmology. A wide range of observations, from galaxy rotation curves to the structure of the cosmic microwave background, concur that about 85% of the matter in the Universe is not ordinary baryonic matter, but some exotic type of weakly interacting particle. At one time, neutrinos were themselves considered as candidates for this mysterious material, but it is now recognised that they travel too close to the speed of light to be consistent with the structure we see in the Universe (when galaxies were forming, neutrinos would be travelling too quickly for the galaxies’ gravity to bind them into orbit, but observations show that the dark matter is bound in galaxies). Nevertheless, it is still possible that neutrinos may help us to solve the dark matter problem.
One of the favoured dark matter candidates is the neutralino, χ, predicted by the (as yet unconfirmed) theory of supersymmetry. If they exist, neutralinos have the right properties for dark matter: they are neutral, stable in most versions of supersymmetry, massive (probably of the order of 100 times the proton’s mass) and weakly interacting. They are produced along with other particles in the very early universe, when the temperature was so high that everything had energies comparable to the beam energy of the Large Hadron Collider, and (being stable) have survived until the present day.
Neutralinos have the interesting property that they are their own antiparticle: two neutralinos can annihilate each other to produce a new particle-antiparticle pair. They cannot produce neutrino-antineutrino pairs directly, but some of the pairs they do produce (such as pairs of Z or W bosons, Higgs particles, or heavy quark-antiquark pairs) can subsequently decay to neutrinos. Therefore, neutrino production would be a possible signature of neutralino annihilation.
The snag is, of course, that as neutralinos are weakly interacting, they do not annihilate one another very easily. If the neutralinos have a mass of 150 GeV, there are something like 3000 of them per cubic metre in the vicinity of the Earth – this sounds like a lot, but it is nowhere near enough to produce a detectable annihilation rate (remember that there are 60 billion solar neutrinos per square centimetre at the Earth, and those are hard enough to detect!). Fortunately, neutralinos can be gravitationally captured by large objects like the Sun, and over time will sink into the Sun’s core: theoretical calculations are inexact, because we have not discovered any supersymmetric particles yet, so we do not know what numbers to put into the equations, but they suggest that it is at least possible that neutralino annihilations in the core of the Sun could produce a detectable neutrino flux in neutrino telescopes. These neutrinos would typically have energies of a few tens to a few hundred GeV, depending on the mass of the neutralino – not as high as the neutrinos from cosmic accelerators, but far higher than neutrinos from fusion or supernova explosions. This neutrino signature would in fact be the only way to detect neutralino annihilation in the Sun’s core – all the other possible annihilation products would be absorbed by the dense matter of the solar interior.



